Fourier series in terms of trigonometric functions

2.1 Fourier series in terms of trigonometric functions

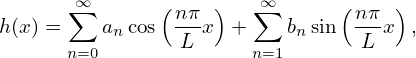
If h(x) is a function of period 2L, then it can be proved that h(x) can be expressed as the following series

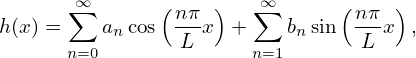∞∑ ( nπ ) ∞∑ (nπ ) h(x ) = ancos L-x + bnsin -L-x , n=0 n=1

(1)

which is called Fourier series. It is not trivial to prove the above statement (what is needed in the proof is to prove that the set of functions cos(nπx∕L) and sin(nπx∕L) with n = 0,1,…∞ is a “complete set”[1]). I will ignore this proof and simply start with Eq. (1).

At this point it is not clear what the coeﬃcients a_n and b_n are. These can be obtained by taking product of Eq. (1) with cos(jπx∕L) and sin(jπx∕L), respectively, and then integrating form −L to L, which gives

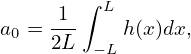1-∫ L a0 = 2L − Lh(x)dx,

(2)

and, for j ≥ 1,

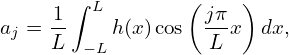1 ∫ L ( jπ ) aj = L- h(x )cos L-x dx, −L

(3)

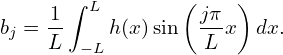( ) 1-∫ L jπ- bj = L −L h(x )sin L x dx.

(4)

In order to enable a_n to be uniformly expressed by Eq. (3), Fourier series are often redeﬁned as

a0 ∑∞ [ ( nπ ) ( nπ ) ] h(x) =-2 + ancos L-x + bn sin L-x . n=1

(5)

[Fourier series (5) can also be written as

∑∞ [ ( ) ( )] h(x) = an-cos nπ-x + bn sin nπx , n=−∞ 2 L 2 L

(6)

where n ranges from −∞ to ∞, and there is no special treatment for the edge case of n = 0. In obtaining expression (6) from (5) , use has been made of a_n cos(nπx∕L) = a_−n cos(−nπx∕L) and b_n sin(nπx∕L) = b_−n sin(−nπx∕L).]

Note that sine and cosine are similar to each other: one can be obtained from the other by shifting, i.e., they diﬀers only in the “phase”. Using trigonometric identities, expression (5) can be expressed in terms of only cosine:

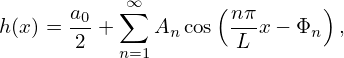a0 ∞∑ (nπ- ) h(x) = 2 + An cos L x− Φn , n=1

(7)

where the amplitude A_n is given by

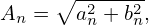∘ -2---2- An = an + bn,

(8)

and the phase Φ_n is given by

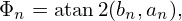Φn = atan2(bn,an),

(9)

where atan2(y,x) is the 2-argument arctangent, which gives an angle in the correct quadrant. Expresion (7) can be stated as: a periodic signal is composed of cosine functions of diﬀerent frequencies and phases (we interpret x as time).

If h(x) is a complex-valued function (the independent variable x is still real number), then the above Fourier expansion can be applied to its real part and imaginary part, respectively. Combining the results, we can see that Eqs. (3)-(5) is still valid. In this case, a_n and b_n are complex numbers.

[next] [front] [up]