[next] [prev] [prev-tail] [tail] [up]

2.2 Fourier series in terms of basis functions einπx∕L

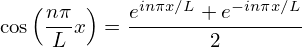
Fourier series are often expressed in terms of the complex-valued basis functions einπx∕L. Next, we derive this version of the Fourier series, which is the most popular version we see in textbooks and papers (we will see why this version is popular).

Using Euler’s formula (this is a bridge between representations using real numbers and complex numbers)

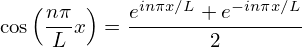(nπ ) einπx∕L + e−inπx∕L cos ---x = ---------------- L 2
(10)

and

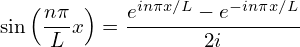( ) inπx∕L −inπx∕L sin nπx = e------−-e------ L 2i
(11)

in Eq. (5), we obtain

[( ) ( ) ] a0 ∞∑ an −-ibn inπx∕L an-+-ibn −inπx∕L h(x) = 2 + 2 e + 2 e . n=1
(12)

Define

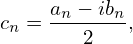an-−-ibn cn = 2 ,
(13)

then, by using a−n = an b−n = −bn, we know that

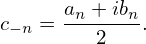c = an +-ibn. −n 2
(14)

Then Eq. (12) is written

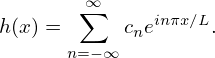∑∞ inπx∕L h(x) = cne . n=−∞
(15)

Using the expressions of an and bn given by Eq. (3) and (4), cn is expressed as

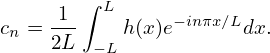1 ∫ L cn = --- h (x)e−inπx∕Ldx. 2L −L
(16)

Equation (15) along with Eq. (16) is the version of Fourier series using complex basis functions. In this version, the index n is an integer ranging from negative infinity to positive infinity, which is unlike Eq. (1), where n is from zero to positive infinity. An advantage of Eqs. (15) and (16) is that no special treatment is needed for the edge case of n = 0.

Using Eq. (16) in Eqs. (15), we obtain

∞∑ ( ∫ L ) h(x) = 1-- h(x)e−inπx∕Ldx einπx∕L. n=−∞ 2L − L ∞∑ ( 1 ∫ L ( (n π ) ( nπ )) ) ( (nπ ) (nπ )) = --- h(x) cos ---x − isin --x dx cos ---x + isin ---x n=−∞ 2L − L L L L L ∞∑ ( 1 ∫ L (nπ ) ) ( nπ ) = --- h(x)cos ---x dx cos --x n=−∞ ( 2L − L L ) L ∞∑ 1 ∫ L (nπ ) (nπ ) + 2L- h(x)sin -L-x dx sin -L-x n=−∞ ( − L ) ∞∑ 1 ∫ L ( nπ ) ( (nπ )) + 2L-− Lh(x) cos L-x dx isin L-x (17) n=−∞ ( ) ∞∑ 1-∫ L ( ( nπ-)) ( (nπ- )) + 2L − Lh(x) − isin L x dx cos L x (18) n=−∞
Noting that the +n terms cancel the −n terms in both line (17) and line (18), the above expression is reduced to
∑∞ ( 1 ∫ L ( nπ ) ) (nπ ) h(x) = --- h(x) cos --x dx cos --x n=−∞ 2L −L L L ∑∞ ( 1 ∫ L ( nπ ) ) ( nπ ) + --- h(x) sin --x dx sin --x (19) n=−∞ 2L −L L L
Define new expansion coefficients
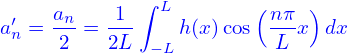∫ L ( ) a′n = an= 1-- h(x)cos nπ-x dx 2 2L − L L
(20)

and

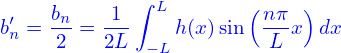∫ L ( ) b′n = bn= 1-- h(x)sin nπ-x dx 2 2L − L L
(21)

then expression (19) is written as

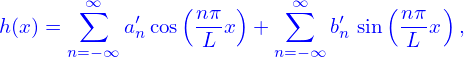∞ ∞ h (x) = ∑ a′cos(n-πx) + ∑ b′ sin (nπ-x), n=−∞ n L n= −∞ n L
(22)

which recovers expression (6). Note that n ∈ (−∞,+∞) in this version, which differs from Eq. (5). Also this expression has no edge case that needs special treatment.

As a benchmark, we can start from exression (6) to derive the complex Fourier expansion: Using the Euler formula in expression (6), we obtain

[( ) ( ) ] ∞∑ an- ibn inπx∕L an- ibn- −inπx∕L h(x) = 4 − 4 e + 4 + 4 e n∞=−∞( ) −∞ ( ) = ∑ an− ibn einπx∕L + ∑ an-+ ibn e−inπx∕L n=1 4 4 n=− 1 4 4 0 ( ) 0 ( ) + ∑ an− ibn einπx∕L + ∑ an-+ ibn- e−inπx∕L n=−∞ 4 4 n=∞ 4 4
Noting that  an = a−n and bn = −b−n, the above expresion is written as
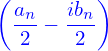h(x)∑ n=−∞∞( ) an-− ibn- 2 2einπx∕L.

Using Eq. (13), the coefficients an and bn appearing in Eq. (5) can be recovered from cn by

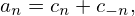an = cn + c−n,
(23)

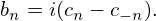b = i(c − c ). n n −n
(24)

If h(x) is real, then the coefficients an and bn are real. Then equation (13) implies that cn and c−n are complex conjugates. In this case, expressions (23) and (24) are simplified as

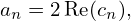an = 2 Re(cn),
(25)

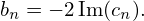bn = − 2Im(cn).
(26)

[In the above, we use the basis functions einπx∕L to expand h(x). If we choose the basis functions to be e−inπx∕L, then it is ready to verify that the Fourier series are written

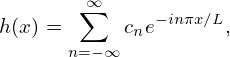∞ h(x) = ∑ c e−inπx∕L, n=− ∞ n
(27)

with cn given by

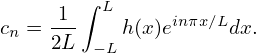1-∫ L inπx∕L cn = 2L − Lh(x)e dx.
(28)

In this case, the coefficients an and bn can be recovered from cn by

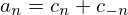an = cn +c− n
(29)

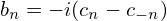bn = − i(cn − c−n )
(30)

In using the Fourier series, we should be aware of which basis functions are used.]

[next] [prev] [prev-tail] [front] [up]