From discrete spectrum to continuous spectrum

B.1 From discrete spectrum to continuous spectrum

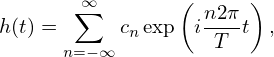
The Fourier series discussed above indicates that a periodic function is composed of discrete spectrum and is written as

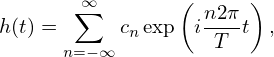∑∞ ( n2π ) h(t) = cnexp i-T-t , n=−∞

(91)

where T is the period of h(t). The nth term of the above Fourier series corresponds to a harmonic of frequency

n fn = T-,

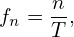(92)

and the expansion coeﬃcient c_n is given by

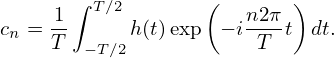1 ∫ T∕2 ( n2π ) cn = T- h(t)exp − i-T-t dt. −T∕2

(93)

In terms of f_n, the coeﬃcient in Eq. (93) is written

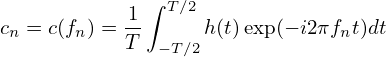∫ T∕2 cn = c(fn) =-1 h(t)exp(− i2πfnt)dt T − T∕2

(94)

In terms of f_n, the Fourier series in Eq. (91) is written

∞∑ h(t) = c(fn)ei2πtfn n=−∞ ∑∞ 1 = T c(fn)ei2πtfn T- (95) n= −∞

Note that c(f_n)e^i2πtf_n is the value of function c(f)e^i2πtf at f = f_n. Further note that the interval between f_n and f_n+1 is 1∕T. Thus the above summation is the rectangular formula for numerically calculating the integration ∫ _−∞^∞c(f)e^i2πtfdf. Therefore, equation (95) can be approximately written as

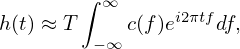∫ ∞ h(t) ≈ T c(f)ei2πtfdf, −∞

(96)

which will become exact when the interval 1∕T → 0, i.e., T →∞. Therefore, for the case T →∞, the Fourier series exactly becomes

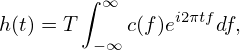∫ ∞ i2πtf h(t) = T −∞ c(f)e df,

(97)

where c(f) is given by Eq. (94), i.e.,

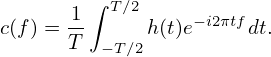-1∫ T∕2 −i2πtf c(f) = T − T∕2 h(t)e dt.

(98)

Note that the function h(t) given in Eq. (97) is proportional to Tc(f) while the function c(f) given in Eq. (98) is proportional to 1∕T. Since T →∞, it is desired to eliminate the T and 1∕T factors in Eqs. (97) and (98), which can be easily achieved by deﬁning a new function

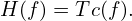H(f) = T c(f).

(99)

Then equations (97) and (98) are written as

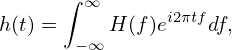∫ ∞ h(t) = H (f )ei2πtfdf, −∞

(100)

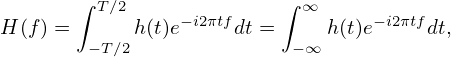∫ T∕2 ∫ ∞ H (f) = h(t)e− i2πtfdt = h(t)e−i2πtfdt, −T∕2 −∞

(101)

Equations (100) and (101) are the Fourier transformation pairs discussed in the next section.

[next] [front] [up]