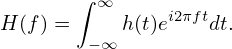
As discussed above, the Fourier transformation of a function h(t) is given by
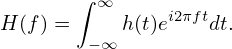 | (102) |
Once the Fourier transformation H(f) is known, the original function h(t) can be reconstructed via
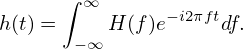 | (103) |
[Note that the signs in the exponential of Eq. (100) and (101) are opposite. Which one should be minus or positive is actually a matter of convention because a trivial variable substitution f′ = −f can change the sign between minus and positive. Proof. In terms of f′, Eq. (103) is written
Define Then Eq. (104) is written
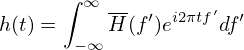 | (106) |
The signs in the exponential of Eqs. (105) and (106) are opposite to Eqs. (102) and (103), respectively.]
[Some physicists prefer to use the angular frequency ω ≡ 2πf rather than the frequency f to represent the Fourier transformation. Using ω, equations. (102) and (103) are written, respectively, as
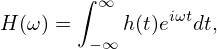 | (107) |
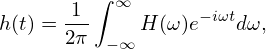 | (108) |
where we see that the asymmetry between the Fourier transformation and its inverse
is more severe in this representation: besides the opposite-sign in the exponents, there
is also a 1∕2π factor difference between the Fourier transformation and its inverse.
Whether the 1∕2π factor appears at the forward transformation or inverse one is
actually a matter of convention. The only requirement is that the product of the two
factors in the forward and inverse transformation is equal to 1∕2π. To obtain a more
symmetric pair, one can adopt a factor 1∕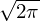 at both the forward and inverse
transformation. The representation in Eqs. (102) and (103) is adopted in
this note. But we should know how to change to the ω representation when
needed.]
at both the forward and inverse
transformation. The representation in Eqs. (102) and (103) is adopted in
this note. But we should know how to change to the ω representation when
needed.]
[
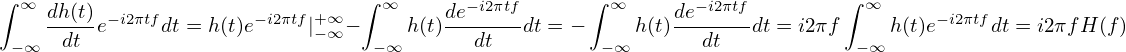 | (109) |
]