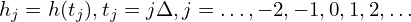
In computational and experimental work, we know only a list of values h(tj) sampled at discrete values of tj. Let us suppose that h(t) is sampled with uniform interval between consecutive points:
|
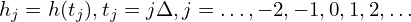| (111) |
The sampling rate is defined by fs = 1∕Δ. The sampling theorem states that: If the Fourier transformation of function h(t), H(f), has the following property
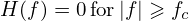 | (112) |
then sampling h(t) with the sampling rate fs ≥ 2fc (i.e., Δ ≤ 1∕(2fc)) will completely determine h(t), which is given explicitly by the formula
![∑∞ sin[2πfc(t−-jΔ)]-
h(t) = Δ hj π(t − jΔ ) .
j=− ∞](fourier_analysis123x.png) | (113) |
We will not concern us here with the proof of the sampling theorem and simply start working with Eq. (113) to derive the concrete expression for the Fourier transformation of h(t). Substituting the expression (113) for h(t) into the Fourier transformation (102), we obtain the explicit form of the Fourier transformation of h(t):
With the help of Wolfram Mathematica, the integration in Eq. (114) is evaluated analytically, giving
![∫ ∞ sin[2πf τ] {
------c--exp(i2πfτ)dτ = 0For |f| > fc .
−∞ πτ 1For |f| < fc](fourier_analysis125x.png) | (115) |
Using this, Eq. (114) is written
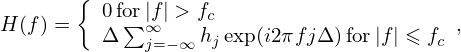 | (116) |
which shows that H(f) = 0 for |f| > fc, which is consistent with the assumption of sampling theorem, i.e., H(f) has the property given in Eq. (112). The second line of Eq. (116) is identical to Eq. (110) except that Eq. (116) in this case is exact while Eq. (110) is only approximate. In other words, if Δ ≤ 1∕(2fc), then the Fourier transformation is exactly given by Eq. (116), where fc is the largest frequency contained in h(t) (i.e., H(f) = 0 for |f| > fc).
![∫ ∞
H (f) ≡ h(t)exp(i2πf t)dt,
− ∞∞ ∫ ∞
= Δ ∑ hj sin[2πfc(t−-jΔ-)]exp (i2πft)dt,
j=−∞ −∞ π(t− jΔ)
∑∞ ∫ ∞
= Δ hjexp(i2πfjΔ) sin[2πfc(t−-jΔ-)]exp[i2πf(t− jΔ)]dt,
j=−∞ −∞ π(t− jΔ)
∑∞ ∫ ∞
= Δ hjexp(i2πfjΔ) sin[2πfcτ]exp[i2πfτ]dτ. (114)
j=−∞ −∞ πτ](fourier_analysis124x.png)