3.2 Periodic property of DFT

We are usually interested in Fourier expansion coefficients in the range n = −N∕2,…,N∕2 (assume that N is even) since we expect the coefficients decay for larger |n| (so we impose a cutoff for a range that is symmetric about n = 0). Then the subscript range of H_n we care about is n ∈. However, the original DFT is for the range n ∈ [0 : N − 1]. How do we reconcile them? The answer is that we make use of the periodic property of DFT. It is obvious that H_n defined in Eq. (34) has the following periodic property:

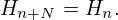(37)

Using this, we can infer what we need: the value of each H_n with n ∈ is equal to H_n with n ∈, respectively. In this scenario, we can associate H_j with the following frequency:

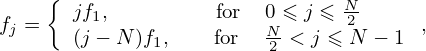(38)

where f₁ = 1∕T.