3.1 Definition

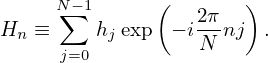
Denote the summation in Eq. (33) by H_n:

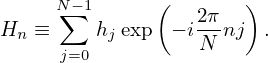(34)

Then H_n with n = 0,1,…N − 1 is called the Discrete Fourier transformation (DFT) of h_j with j = 0,1,…,N − 1. (The efficient algorithm of computing the DFT is discussed in Appendix A.)

Why do we choose n to be in the positive range [0 : N − 1]? This is to make the tranform pair symmetric: both j and n are in the same range. This symmetry is helpful in making the transform pair easy to remember. This does not mean we only need the positive frequency components. In fact, we usually need n in the range [−N∕2,N∕2]. This will be discussed in the next section.

In terms of H_n, the Fourier expansion coefficients c_n in Eq. (33) is written as

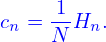(35)

The corresponding frequency is

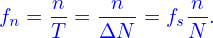(36)

Here f₁ is called the fundamental frequency (spacing in the frequency domain).