Reconstruct the original function using DFT

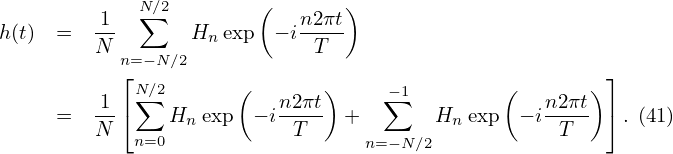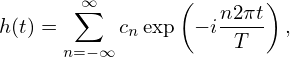
The Fourier series of h(t)

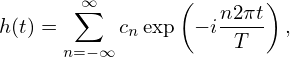∑∞ ( n2 πt) h(t) = cnexp − i-T- , n=−∞

(39)

can be approximated as

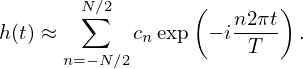N∕2 ( ) h(t) ≈ ∑ c exp − in2πt . n T n= −N∕2

(40)

Using the relation c_n = H_n∕N, the above equation is written as

N∑∕2 ( ) h(t) = 1- Hn exp − in2πt N n=−N ∕2 T ⌊N ∕2 ( ) − 1 ( )⌋ = 1-⌈∑ H exp − in2-πt + ∑ H exp − in2πt ⌉ .(41) N n=0 n T n=− N∕2 n T

Using the periodic property of DFT, i.e., H_n = H_N+n, the above expression is written as

⌊N∑∕2 ( ) N∑−1 ( )⌋ h(t) = 1-⌈ Hn exp − in2πt + Hn exp − i(n-− N-)2πt ⌉(.42) N n=0 T n=N∕2 T

Equation (42) provides a formula of constructing an approximate function using the DFT of the discrete samplings of the original function.