Coordinate system and grid in TEK code

D Coordinate system and grid in TEK code

In (ψ,𝜃,ϕ) coordinates:

ψ is the normalized poloidal magnetic ﬂux, ψ = (Ψ − Ψ_axis)∕(Ψ_lcfs − Ψ_axis).
𝜃 ∈ [−π,π) is increasing along the anti-clockwise direction when viewed along ∇ϕ direction with 𝜃 = −π at the high-ﬁeld-side midplane.
ϕ is the toroidal angle of the right-handed cylindrical coordinates (R,ϕ,Z).

In this convention, the Jacobian of the (ψ,𝜃,ϕ) coordinate system, 𝒥 = (∇ψ ⋅∇𝜃 ×∇ϕ) is negative, i.e., (ψ,𝜃,ϕ) is a left-handed system. The ﬁeld-line-following coordinate system (ψ,𝜃,α) is also a left-handed system. The coordinate system (x = ψ,y = α,z = 𝜃) is a right-handed system.

D.1 Poloidal grid

Fig. 11: Poloidal grid for equilibrium quantities used in TEK and GEM code. The array starts at 𝜃 = −π and ends at 𝜃 = +π (𝜃 = ±π is chosen to be at the high-ﬁeld side midplane in both the codes). TEK array index starts from 1 whereas GEM array index starts from 0. Hence mpol=nth+1. nth is denoted by ntheta in GEM. In TEK, mpol must be an odd number, so that the array has a midpoint indexed by (mpol+1)/2, which corresponds to 𝜃 = 0.

I do not need to make connection with GEM’s equilibrium poloidal array because there is no coupling of equilibrium quantities between the code written by me and the original code in GEM. The coupling happens for the perturbed quanties, whose poloidal grids need to be consistent.

The gridpoint number along 𝜃 for perturbations is denoted by mpol2. Its value is not chosen by users. Instead, it is equal to numproc/ntube, i.e., mpol2 is the total number of cells along 𝜃 for MPI parallelation. (numproc and ntube must be chosen in a way that makes numproc/ntube an integer.)
Poloidal grid-points for perturbations are indexed as 0:mpol2-1, with 0 corresponding to 𝜃 = −π and mpol2 corresponding to 𝜃 = π. Field equations are solved at 0 : mpol2 − 1. (The ﬁeld at mpol2, i.e., 𝜃 = +π, is not identical to that at 𝜃 = −π due to toroidal shift of a magnetic ﬁeld line when it ﬁnish one poloidal loop, and is obtained by toroidally inerpolating the ﬁelds at 𝜃 = −π.) No array for this is actually used in the code. The indexes just correspond to gclr of MPI processors.
The equilibrium poloidal gridpoint number, mpol, must be chosen in a way that makes (mpol-1)/mpol2 an integer, which can be larger than 1, i.e., one simulation cell can span several equilibrium cells.

D.2 Toroidal grid

pict

Fig. 12: Toroidal grid used in TEK and GEM. In TEK, the toroidal array is tor_1d_array(1:mtor+1). Source terms, δn and δj_∥, and EM ﬁelds are deﬁned at 1:mtor. GEM array index starts from 0 and ends at jm. It follows that mtor=jm.

D.3 Radial grid

pict

Fig. 13: Radial grid used in TEK. Two radial arrays are used in the code, radcor_1d_array(1:nt) and radcor_1d_array2(1:n), equilibrium is deﬁned on the former grid, and perturbations are deﬁned on the latter grid. Here nt = n + 2m, m is the number of grid points in one of the two buﬀer regions (regions in blue color). In the code n is denoted by nflux2 and nt is denoted by nflux, m is denoted by points_in_buffer. In GEM the radial array does no include the buﬀer regions and the index starts at 0 and ends at imx. Hence n=imx+1.

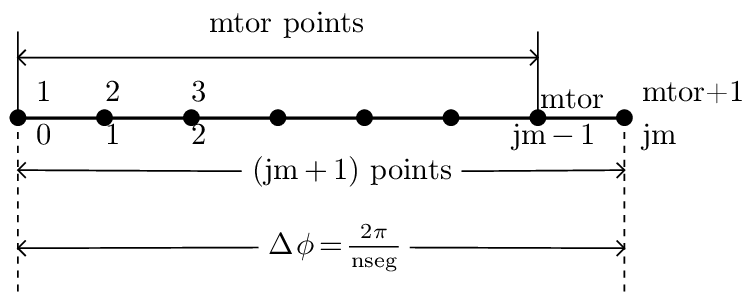
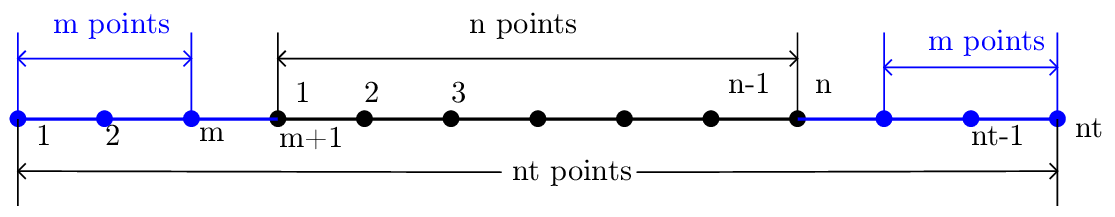
GEM array index system is better than TEK’s because my system is not consistent: sometimes I use 0-based index and sometimes I use 1-based index, sometimes the index ends at n and sometimes ends at n+1. It is important to know accurately the transformation between the two systems.

[next] [prev] [prev-tail] [front] [up]