[next] [prev] [prev-tail] [tail] [up]

C From (δΦ,δA) to (δE,δB)

C.1 Expression of δB⊥ in terms of δA

Note that

δB ⊥ = ∇ × δA − (e∥ ⋅∇ × δA )e∥ = ∇ × (δA ⊥ + δA∥e∥)− [e∥ ⋅∇ × (δA ⊥ +δA ∥e∥)]e∥ (319)

Correct to order O(λ), δB⊥ in the above equation is written as (e∥ vector can be considered as constant because its spatial gradient combined with δA will give terms of O(λ2), which are neglected)

δB⊥ ≈ ∇ × δA ⊥ + ∇ δA∥ × e∥ − [e∥ ⋅∇ × δA ⊥ + e∥ ⋅(∇ δA∥ ×e∥)]e∥ (320) = ∇ × δA + ∇ δA × e − (e ⋅∇ × δA )e (321) ⊥ ∥ ∥ ∥ ⊥ ∥

Using local cylindrical coordinates (r,ϕ,z) with z being along the local direction of B0, and two components of A⊥ being Ar and Aϕ, then ∇× A⊥ is written as

( ∂δAϕ ) (∂δAr ) 1 [ ∂ ∂δAr ] ∇ × δA ⊥ = − -∂z-- er + -∂z-- eϕ + r ∂r(rδAϕ)− -∂-ϕ- e∥.
(322)

Note that the parallel gradient operator ∇∥≡ e∥⋅∇ = ∂∕∂z acting on the the perturbed quantities will result in quantities of order O(λ2). Retaining terms of order up to O(λ), equation (322) is written as

[ ] ∇ ×δA ⊥ ≈ 1 ∂-(rδAϕ)− ∂-δAr- e∥, r ∂r ∂ ϕ
(323)

i.e., only the parallel component survive, which exactly cancels the last term in Eq. (321), i.e., equation (321) is reduced to

δB⊥ = ∇ δA ∥ × e∥.
(324)

Using basis vectors in field-aligned coordinates

In terms of δBxL and δByL,  δB⊥ is written as

δB ⊥ = δBxL∇x + δByL ∇y = ∇δA ∥ × e∥
(325)

Dotting the above equation by ∇x and ∇y, respectively, we obtain

δBxL|∇x|2 + δByL∇x ⋅∇y = ∇x ⋅(∇ δA∥ × e∥),
(326)

2 δBxL∇x ⋅∇y + δByL|∇y |= ∇y ⋅(∇ δA∥ × e∥).
(327)

Equations (326) and (327) can be further written as

( ∂δA∥ ∂δA∥ ) δBxL|∇x|2 + δByL∇x ⋅∇y = − ∇x ⋅ -∂y-∇y × e∥ + -∂z-∇z × e∥ ,
(328)

and

2 ( ∂δA∥- ∂δA∥- ) δBxL∇x ⋅∇y + δByL |∇y | = − ∇y ⋅ ∂x ∇x × e∥ + ∂z ∇z × e∥ ,
(329)

The solution of this 2 × 2 system is expressed by Cramer’s rule in the code.

 

Use B0 = Ψ′∇x ×∇y

b = Ψ′∇x ×∇y∕B0

C.2 Expression of δB∥ in terms of δA

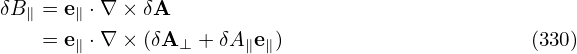
δB∥ = e∥ ⋅∇ × δA = e∥ ⋅∇ × (δA ⊥ + δA∥e∥) (330)

Accurate to O(λ1), δB∥ in the above equation is written as (e∥ vector can be considered as constant because its spatial gradient combined with δA will give O(λ2) terms, which are neglected)

δB ≈ e ⋅∇ × δA + e ⋅(∇ δA ×e ) ∥ ∥ ⊥ ∥ ∥ ∥ = e∥ ⋅∇ × δA ⊥ (331)

[Using local cylindrical coordinates (r,ϕ,z) with z being along the local direction of B0, and two components of δA⊥ being δAr and δAϕ, then ∇× δA⊥ is written as

( ) ( ) [ ] ∂δA-ϕ ∂δAr- 1 ∂-- ∂δAr- ∇ × δA⊥ = − ∂z er + ∂z er + r ∂r(rδAϕ)− ∂ϕ e∥
(332)

Note that the parallel gradient operator ∇∥≡ e∥⋅∇ = ∂∕∂z acting on the the perturbed quantities will result in quantities of order O(λ2). Retaining terms of order up to O(λ), equation (322) is written as

[ ] 1 ∂-- ∂-δAr- ∇ ×δA ⊥ ≈ r ∂r(rδAϕ)− ∂ ϕ e∥,
(333)

Using this, equation (331) is written as

1[ ∂ ∂δA ] δB∥ = - --(rδA ϕ)− ----r . r ∂r ∂ϕ
(334)

However, this expression is not useful for GEM because GEM does not use the local coordinates (r,ϕ,z).]

 

C.3 Expressing the perturbed drift in terms of δE and δB

The perturbed drift δVD is given by Eq. (138), i.e.,

δVD = −-q∇X ⟨δL⟩α × e∥. m Ω
(335)

Using δL = δΦ − v ⋅ δA, the above expression can be further written as

q e∥ δVD = −m-∇X ⟨δΦ − v⋅δA ⟩α × Ω- q-e∥ q-e∥ = m Ω ×∇X ⟨δΦ⟩α − m Ω ×∇X ⟨v∥δA∥⟩α -q e∥ −m Ω × ∇X ⟨v⊥ ⋅δA ⊥⟩α. (336)

Accurate to order O(λ), the term involving δΦ is

-q e∥× ∇ ⟨δΦ⟩ = e∥-×⟨∇ δΦ⟩ m Ω X α B0 X α ≈ e∥-×⟨∇ δΦ⟩ B0 ⟨ x α ⟩ e∥- ∂δA- ≈ B0 × − δE − ∂t α e∥ ≈ B--×⟨− δE⟩α ≡ δV0 , (337) E

which is the δE×B0 drift. Accurate to O(λ), the ⟨v∥δA∥⟩α term on the right-hand side of Eq. (336) is written

q e∥ q v∥ −m- Ω-× ∇X ⟨v∥δA ∥⟩α ≈ − m-Ω-⟨e∥ × ∇X (δA∥)⟩α q v∥ ≈ − m-Ω-⟨e∥ × ∇x (δA ∥)⟩α (338) ⟨δB⊥ ⟩α = v∥--B----, (339) 0

which is called “magnetic fluttering” (this is actually not a real drift). In obtaining the last equality, use has been made of Eq. (324), i.e., δB⊥ = ∇xδA∥× e∥.

Accurate to O(λ), the last term on the right-hand side of expression (336) is written

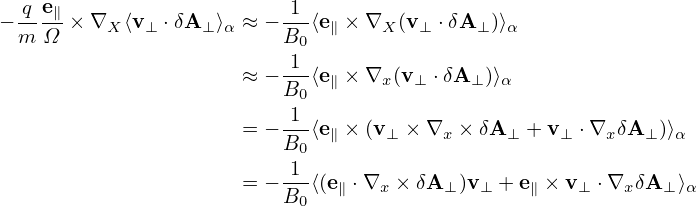
e − q--∥× ∇X ⟨v⊥ ⋅δA⊥ ⟩α ≈ − 1-⟨e∥ × ∇X (v⊥ ⋅δA⊥ )⟩α m Ω B0 ≈ − 1-⟨e∥ × ∇x (v ⊥ ⋅δA ⊥)⟩α B0 = − 1-⟨e × (v × ∇ ×δA + v ⋅∇ δA )⟩ B0 ∥ ⊥ x ⊥ ⊥ x ⊥ α 1-- = − B0⟨(e∥ ⋅∇x × δA⊥ )v ⊥ + e∥ × v ⊥ ⋅∇x δA⊥ ⟩α

Using equation (331), i.e., δB∥ = e∥⋅∇× δA⊥, the above expression is written as

−-q e∥× ∇X ⟨v⊥ ⋅δA⊥⟩α = − 1-⟨δB∥v⊥ + e∥ × v⊥ ⋅∇xδA ⊥⟩α m Ω B0 ≈ − 1-⟨δB v + e × v ⋅∇ δA ⟩ B0 ∥ ⊥ ∥ ⊥ X ⊥ α 1-- -1- ≈ − B0⟨δB∥v⊥ ⟩α − B0e∥ × ⟨v ⊥ ⋅∇X δA ⊥⟩α. 1-- ≈ − B0⟨δB∥v⊥ ⟩α. (340)

where use has been made of ⟨v⊥⋅∇XδA⊥⟩α ≈ 0 (**seems wrong**), where the error is of O(λ)δA⊥. The term ⟨δB∥v⊥⟩α∕B0 is of O(λ2) and thus can be neglected (I need to verify this).

Using Eqs. (337), (339), and (340), expression (336) is finally written as

q- e∥ ⟨δE⟩α ×-e∥ ⟨δB-⊥⟩α- δVD ≡ − m ∇X ⟨δL ⟩α × Ω = B0 + v∥ B0 .
(341)

Using this, the first equation of the characteristics, equation (305), is written as

dX -dt = v∥e∥ + VD + δVD (342) ⟨δE⟩α × e∥ ⟨δB ⟩ = v∥e∥ + VD + ----------+ v∥---⊥-α- B0 B0 ≡ VG (343)

C.4 Expressing the coefficient before ∂F0∕∂𝜀 in terms of δE and δB

[Note that

∂δA⊥- ∂t = − (δE ⊥ + ∇⊥δΦ ),
(344)

where ∂δA⊥∕∂t is of O(λ2). This means that δE⊥ + ∇⊥δϕ is of O(λ2) although both δE⊥ and δϕ are of O(λ).]

Note that

∂⟨v ⋅δA⟩α ∂⟨δA∥⟩α ∂ ⟨δA ⟩α ----∂t--- = v∥--∂t---+ v ⊥ ⋅--∂t-- ∂⟨δA ⟩ = v∥----∥-α+ ⟨v⊥ ⋅(− δE − ∇δΦ )⟩α ∂t ≈ v∥∂⟨δA∥⟩α− ⟨v⊥ ⋅δE⟩α (345) ∂t

where use has been made of ⟨v⊥⋅∇δϕ⟩≈ 0, This indicates that ⟨v⊥⋅δE⟩α is of O(λ1)δE. Using Eq. (345), the coefficient before ∂F0∕∂𝜀 in Eq. (143) can be further written as

[ ( ) ] − q- − ∂-⟨v-⋅δA⟩α − v e + V − q-e∥× ∇ ⟨v ⋅δA ⟩ ⋅∇ ⟨δΦ⟩ m ∂t ∥ ∥ D m Ω X α X α q [ ∂⟨δA ∥⟩α ( q e∥ ) ⟨ ∂δA ⟩ ] = − m- − v∥--∂t-- + ⟨v⊥ ⋅δE ⟩α − v∥e∥ + VD − m-Ω-× ∇X ⟨v ⋅δA ⟩α ⋅ − δE −-∂t- [ ( ) ⟨ α ⟩ ] ≈ − q- − v∥∂⟨δA-∥⟩α + ⟨v⊥ ⋅δE ⟩α − v∥e∥ + VD − q-e∥× ∇X ⟨v ⋅δA ⟩α ⋅⟨− δE⟩α + v∥ ∂A∥ m [ ∂t ( m Ω ) ] ∂t α = − q- ⟨v ⊥ ⋅δE ⟩α + v∥e∥ + VD −-q e∥× ∇X ⟨v⋅δA ⟩α ⋅⟨δE⟩α m [ ( m Ω ) ] ≈ − q- ⟨v ⋅δE ⟩ + v e + V + v ⟨δB-⊥⟩- ⋅⟨δE⟩ . (346) m ⊥ α ∥ ∥ D ∥ B0 α

Using Eq. (346) and (), gyrokinetic equation (143) is finally written as

[ ( ) ] ∂- + v∥e∥ + VD + ⟨δE-⟩α-×-e∥+ v∥⟨δB⊥-⟩α ⋅∇X δf ∂t B0 B0 (⟨δE⟩α-×-e∥ ⟨δB⊥-⟩α-) = − B0 + v∥ B0 ⋅∇XF0 q [ ( ⟨δB ⟩ ) ] ∂F − -- ⟨v⊥ ⋅δE ⟩α + v∥e∥ + VD + v∥---⊥-α- ⋅⟨δE⟩α ---0. (347) m B0 ∂𝜀

 

 

 

[next] [prev] [prev-tail] [front] [up]