[next] [prev] [prev-tail] [tail] [up]

4 Code Benchmarking

4.1 Initial conditions

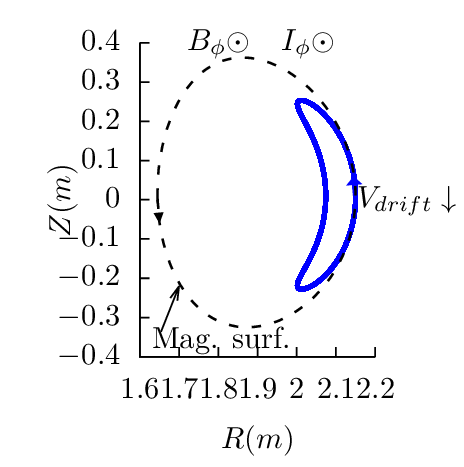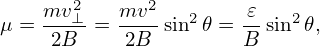
The initial conditions of the particle are given by specifying the initial location (R,ϕ,Z), initial parallel velocity v∥, and the magnetic moment μ (which acts as a parameter since μ is exactly conserved). In some cases, we prefer to specify the initial velocity in terms of the initial kinetic energy 𝜀 and the initial pitch angle 𝜃 (the include angle between velocity and the local magnetic field). The relation between (𝜀,𝜃) and (v∥,μ) is given by

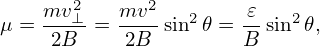mv2⊥ mv2- 2 𝜀- 2 μ = 2B = 2B sin 𝜃 = B sin 𝜃,
(53)

and

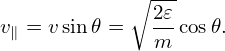∘ 2𝜀- v∥ = vsin 𝜃 = m- cos𝜃.
(54)

The relation between (𝜀,𝜃) and the normalized quantities (μ,v∥) is given by

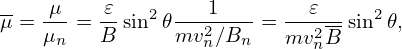μ-= -μ-= -𝜀sin2𝜃---1----= --𝜀---sin2𝜃, μn B mv2n∕Bn mv2nB
(55)

and

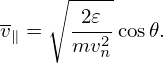∘ ----- - 2𝜀 v∥ = mv2-cos𝜃. n
(56)

4.2 Constants of motion

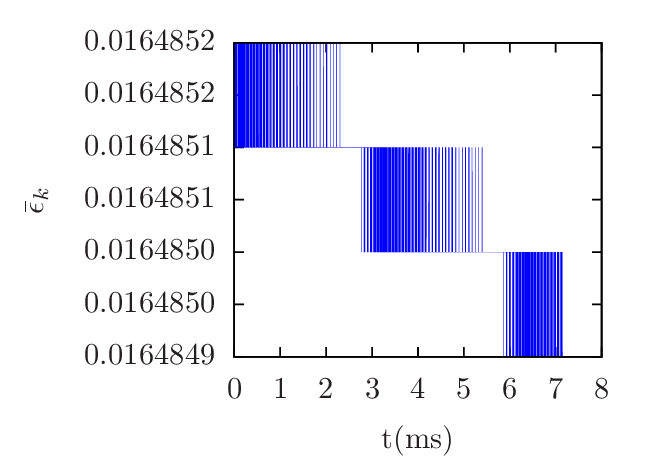
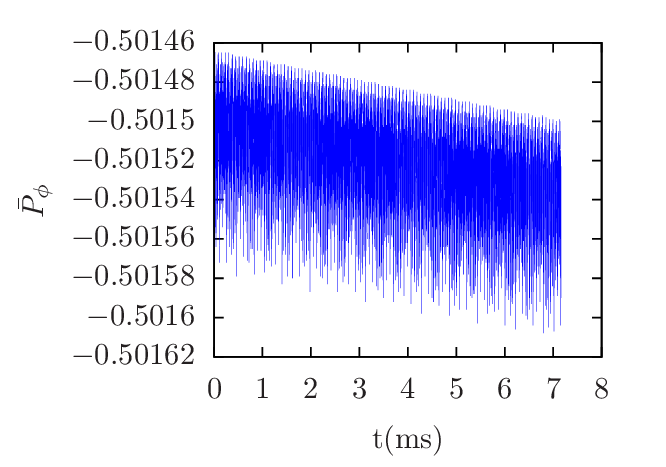
There are three constants of motion for the guiding center motion, namely, the canonical toroidal angular momentum Pϕ, the magnetic moment μ, and the total kinetic energy 𝜀. Examining how well the kinetic energy 𝜀 and the toroidal angular momentum Pϕare conserved provides a way to evaluate the accuracy of the numerical code. The kinetic energy 𝜀 and toroidal angular momentum Pϕ are defined by

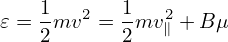1 1 𝜀 = -mv2 = -mv2∥ + B μ 2 2
(57)

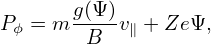g(Ψ ) Pϕ = m -B--v∥ + ZeΨ,
(58)

Define 𝜀n = mvn2 and Pϕn = ZeBnLn2, then the normalized forms of 𝜀 and Pϕ are written as

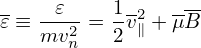- 𝜀 1-2 --- 𝜀 ≡ mv2-= 2v∥ + μB n
(59)

-- P ϕ Pϕ ≡ P--- ϕnv -- = 1-g-∥-+ Ψ (60) 2π B
Figure 6 plots the time evolution of the kinetic energy 𝜀 and toroidal angular momentum Pϕ for an energetic ion in EAST magnetic configuration. The results shows that 𝜀 and Pϕ are conserved to acceptable accuracy for 100 poloidal periods of the orbit.

pict pict pict

Figure 6: Time evolution of the kinetic energy 𝜀 (a) and toroidal angular momentum Pϕ (b) for a Deuteron of 20keV launched at the low-field-side midplane (Rini = 2.15m,Zini = 0m) with pitch angle 𝜃 = 75∘. The results shows that 𝜀 and Pϕ are conserved to acceptable accuracy (𝜀k decreased by 1.8 × 10−5 and Pϕ by 3.2 × 10−4 during the time of 100 poloidal periods). The corresponding poloidal orbit is plotted in (c). Fourth-order Runge-Kutta time advancing scheme is used in integrating the orbit with a time step of 1∕183 poloidal period. The magnetic equilibrium is from EAST discharge #62585@2.8s (gfile provided by ZhengZheng).

[next] [prev] [prev-tail] [front] [up]