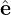 R(ϕ) + Z
R(ϕ) + Z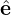 Z. Using this, we obtain
Z. Using this, we obtain In this section, all quantities are in the normalized form given in Sec. 1.1. For notational simplicity, the
over-bars of the notation are omitted. In cylindrical coordinates (R,ϕ,Z), the location vector is written
as X = R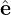 R(ϕ) + Z
R(ϕ) + Z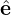 Z. Using this, we obtain
Z. Using this, we obtain
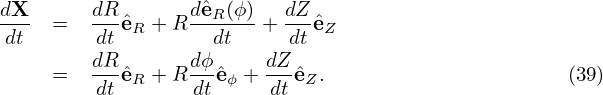
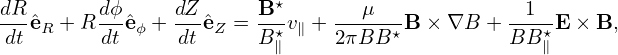 | (40) |
from which we obtain the following component equations:
![[ ⋆ ]
dR-= B--v∥ +---μ---B × ∇B + --1- E× B ⋅ˆeR
dt B ⋆∥ 2πBB ⋆∥ BB ⋆∥](guiding_center_motion52x.png) | (41) |
![[ ]
dZ- B-⋆ ---μ--- --1-
dt = B ⋆v∥ + 2πBB ⋆B × ∇B + BB ⋆E × B ⋅ˆeZ,
∥ ∥ ∥](guiding_center_motion53x.png) | (42) |
![dϕ 1 [B ⋆ μ 1 ]
---= -- --⋆v∥ +-----⋆-B ×∇B + ---⋆E × B ⋅ˆeϕ,
dt R B ∥ 2πBB ∥ BB ∥](guiding_center_motion54x.png) | (43) |
In the cylindrical coordinates, the terms B ×∇B, ∇× b, and b ⋅∇× b are written, respectively, as
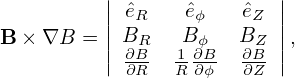 | (44) |
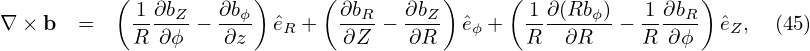
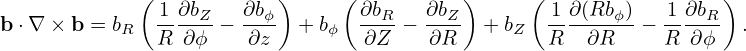 | (46) |
Using bR = 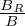 , bZ =
, bZ = 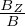 , and bϕ =
, and bϕ = 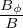 , we obtain
, we obtain
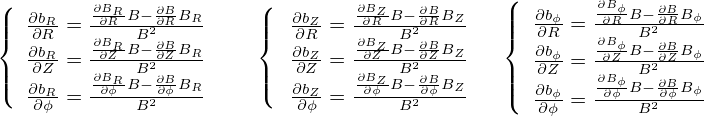 | (47) |
The equation for v∥ is given by Eq. (11), i.e.,
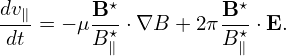 | (48) |
The first term on the left-hand-side is written
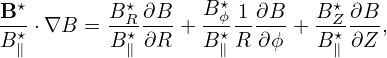 | (49) |
where
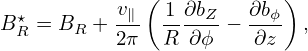 | (50) |
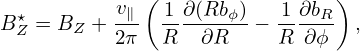 | (51) |
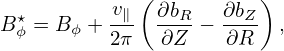 | (52) |
and B∥⋆ is given by Eq. (13).