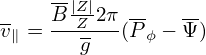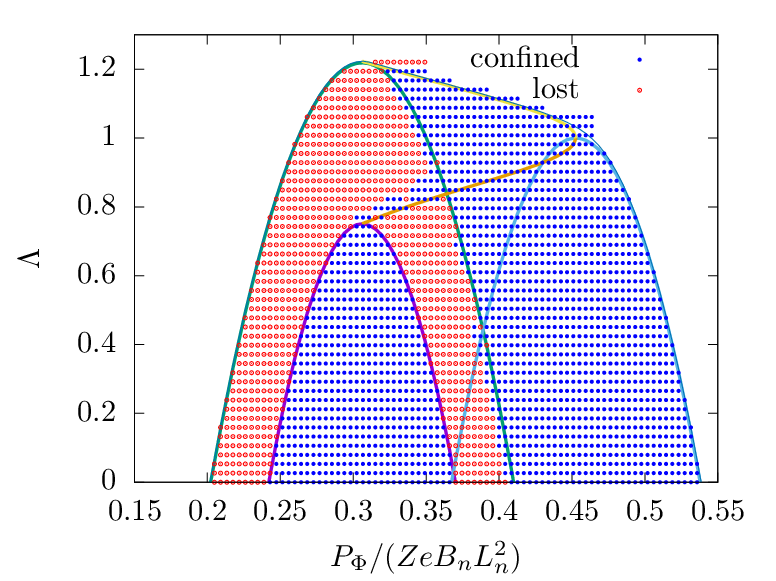
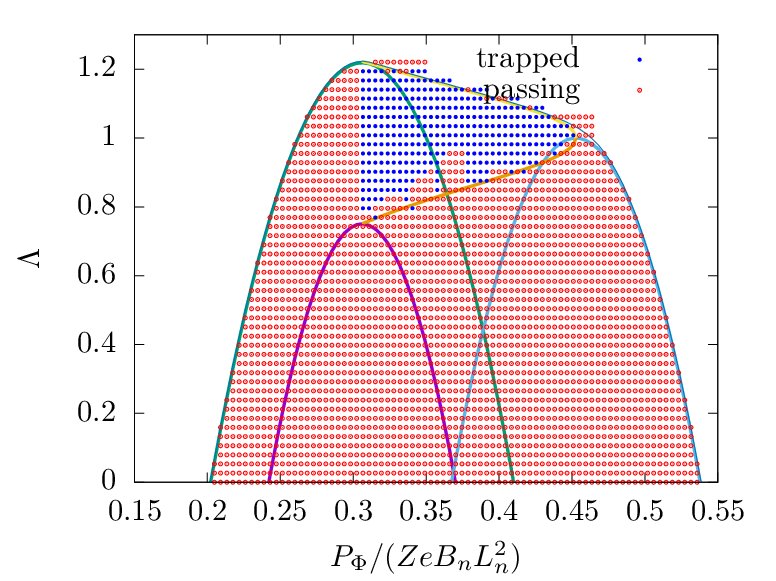
Figure 11: For E = 50keV, EAST#52340. Orbits are numerically computed to check whether
they are confined (not touch the LCFS) or lost (touch the LCFS). Some particles in the loss
region are numerically determined to be confined. Whether this is due to numerical errors is
unclear.
 (
(