Trapped passing boundary in the zero-orbit-width limit

5.2 Trapped passing boundary in the zero-orbit-width limit

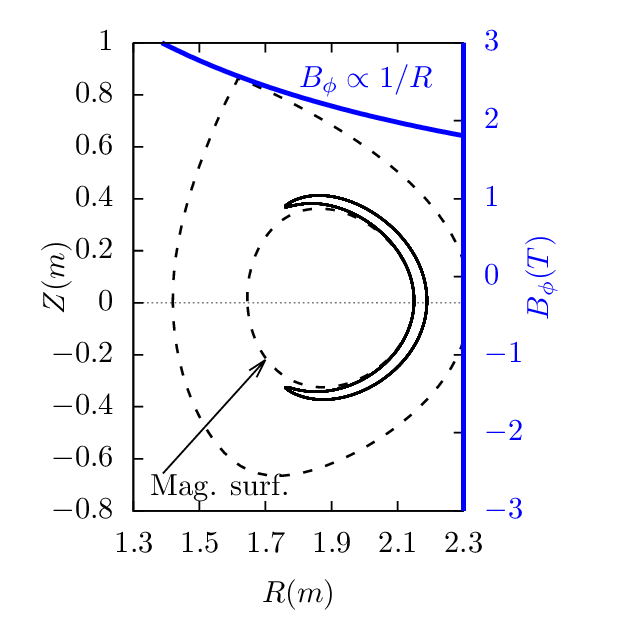
An approximate condition determining whether a particle is trapped or circulating can be obtained by using the conservation of magnetic moment and kinetic energy, and assuming the guiding center orbit is along the magnetic ﬁeld line (zero-width orbit approximation, which is a proper approximation for low-energy particles whose orbit width is small, as is shown in Fig. 13).

pict

Figure 13: The magnetic ﬁeld becomes stronger when a particle move inboard (toward smaller R). Due to the conservation of kinetic enery and magnetic moment, the magnitude of the paralell velocity decrease when a particle moves inboard. Also shown is the poloidal projection of guiding-center orbit for a particle of energy 2keV launched in the low-ﬁeld-side midplane (R = 2.25m,Z = 0m) with a pitch angle 𝜃 = 115^∘.

In this approximation, the orbit remains on a magnetic surface. The critical condition for a particle to be trapped/circulating is given by

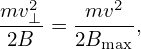mv2⊥ -mv2-- 2B = 2Bmax ,

(76)

where v_⊥ is the perpendicular (to the magnetic ﬁeld) velocity of the particle at the location where the strength of the magnetic ﬁeld is B, B_max is the maximum value of the magentic ﬁeld on the same magnetic surface where the particle moves. Deﬁne 𝜃 = arccos(v_∥∕v), which is the pitch angle of velocity with respect to the local magnetic ﬁeld, then Eq. (76) is written as

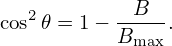2 --B-- cos 𝜃 = 1− Bmax .

(77)

Deﬁne

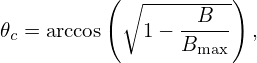( ) ∘ -----B--- 𝜃c = arccos 1− Bmax- ,

(78)

then particles with 𝜃_c < 𝜃 < π − 𝜃_c can not reach the point of the maximum magnetic ﬁeld of the same magnetic surface and thus they are trapped particles. Otherwise, they are circulating particles. In velocity space (v_∥,v_⊥), the trapped and circulating region are shown in Fig. 14.

pict

Figure 14: Passing and trapped regions in the phase-space (v_∥,v_⊥). The trapped region is 𝜃_c < 𝜃 < π − 𝜃_c.

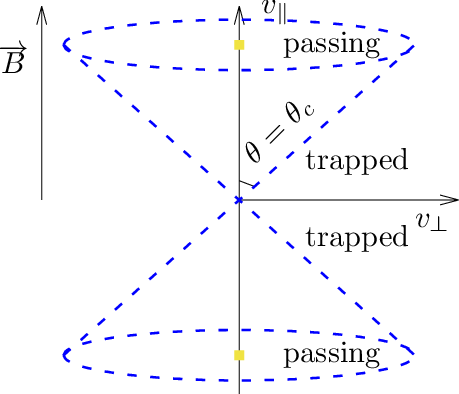
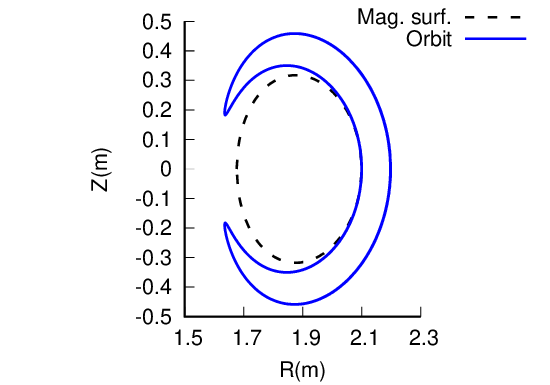
Note that the trapped-circulating boundary given in Fig. 14 is determined based on the assumption that the guiding center motion does not deviate from a magnetic surface. However, the actual guiding center orbit does not remain on the same magnetic surface, so the above result can be wrong when applied to some particles. An example is given in Fig. 15, where the numerical results show that the particle is actually trapped but the approximate condition indicate that the particle is circulating.

pict

Figure 15: Numerical orbit of a particle on the poloidal plane, which show that the particle is trapped. However, the particle would be considered to be circulating if we used the approximate condition given in Fig. 14. It is easy to understand why the approximate condition breaks down for this case: the orbit derivates from the original ﬂux surface (i.e., the zero-width orbit) to the stronger ﬁeld region.

At a given radial location, in terms of (w,μ) coordinates, where w is the kinetic energy, the trapped passing boundary is shown in Fig. 16.

pict

Figure 16: The passing and trapped regions of phase space (w,μ). The boundary between passing and trapped region is given by w = μB_max, where B_max is the maximum value of magnetic ﬁeld on the same magnetic surface where the particle moves (zero orbit width is assumed).

[next] [prev] [prev-tail] [front] [up]