[next] [prev] [prev-tail] [tail] [up]

5.3 Trapped particle fraction

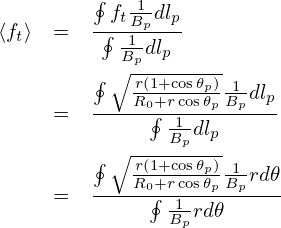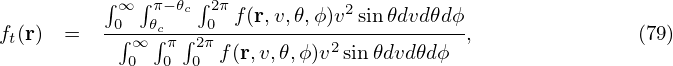
The trapped particle fraction ft is defined as the ratio of the number of trapped particles to the total number of particles. Particle distribution function (in terms of guiding-center variables) can be written as f = f(r,v,𝜃,ϕ), where r is the guiding-center position vector in configuration space and (v,𝜃,ϕ) is the spherical coordinates in velocity space with 𝜃 being the pitch angle and ϕ the gyro-angle. Assuming zero Larmor radius limit, then the trapped particle fraction ft is written as

∫ ∞ ∫π−𝜃c∫2πf(r,v,𝜃,ϕ)v2 sin𝜃dvd𝜃dϕ ft(r) = -0∫∞-𝜃c∫π-∫20π----------------------, (79) 0 0 0 f(r,v,𝜃,ϕ)v2sin𝜃dvd𝜃dϕ
where 𝜃c is the critical pitch angle defined in Sec. 5. Assume that f(r,v,𝜃,ϕ) is uniform in 𝜃 and ϕ, then the integration over the 𝜃 and ϕ in Eq. (79) can be performed, giving
∫ ∞ 2 ft(r) = 2π×-2co∫s𝜃∞c-0--f(r,v)v-dv 4π 0 f (r,v)v2dv = cos𝜃c. (80)
Using the definetion of the critical value of the pitch angle (Eq. (78)), the above expression is written as
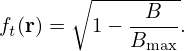∘ --------- ft(r) = 1− -B---. Bmax
(81)

The flux surface averaging of ft, ⟨ft⟩, is written as

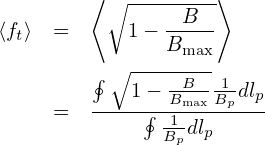
⟨∘ --------⟩ ⟨ft⟩ = 1 − -B--- Bmax ∮ ∘-----B---1 = ---1-−∮-BmaxBpdlp B1p dlp
How to relate ⟨ft⟩ to the following neoclassical effective trapped fraction?
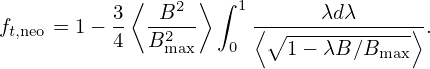3 ⟨ B2 ⟩ ∫ 1 λdλ ft,neo = 1− 4 B2--- ⟨∘------------⟩-. max 0 1 − λB ∕Bmax
(82)

5.3.1 For circular flux sruface with large aspect ratio

In the large aspect ratio approximation and for particles that are initially on the low-field-side of the midplane, Eq. (81) is written

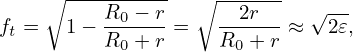∘ ---------- ∘ ------ R0-−-r --2r-- √-- ft = 1− R0 + r = R0 + r ≈ 2𝜀,
(83)

where 𝜀 = r∕R0. This is the result given in Wessson’s book[2]. Note that this result is valid only for particles that are initially at the low-field-side of the midplane. For particles that are initially located at the poloidal location 𝜃p, the trapped particles fraction is written

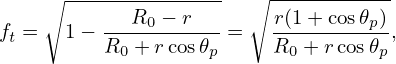----------- ∘ ------R-−-r---- ∘ r(1 +cos𝜃 ) ft = 1− ----0------= ---------p-, R0 + rcos𝜃p R0 + rcos𝜃p
(84)

For 𝜃p = π, i.e., at the high-field-side of the midplane, ft = 0, i.e., there is no trapped particles there.

Using Eq. (84), the flux surface averaging of ft, ⟨ft⟩, is written as

∮ --ft 1Bpdlp ⟨ft⟩ = ∮ 1-dlp ∮ ∘Bp-------- rR(10++crocsos𝜃p𝜃)pB1p dlp = -----∮--1-------- ∘ ---Bpdlp- ∮ r(1+cos𝜃p)-1 rd𝜃 = ----R0∮+rc1os𝜃pBp---- Bprd𝜃

[next] [prev] [prev-tail] [front] [up]