5.6 Methods of determining drift orbits
If neglecting the magnetic drift, a guiding-center orbit is along a magnetic field lines, i.e., there is no
derivation from the magnetic surface where a guiding center is initially located. Taking the magnetic
drift into account, a guiding-center orbit will deviate from the initial magnetic surface, giving an orbit
of nozero width in the poloidal plane.
Whether a guiding-center will drift radially outward or inward from a local magnetic surface near
the midplane can be determined in the following way. First note that the zero-order approximation of
the guiding-center orbit (zero-width orbit) is either parallel or anti-parallel to the local magnetic field,
depending on the sign of v∥. Further note the direction of the magnetic drift (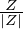 B×∇B and curvature
drift) is approximatedly vertical, which can be either up or down, depending on the charge sign and
direction of the toroidal magnetic field. Finally, by imposing the magnetic drift on the zero-width orbit,
we can determine whether the guiding center will drift inward or outward from the local magnetic
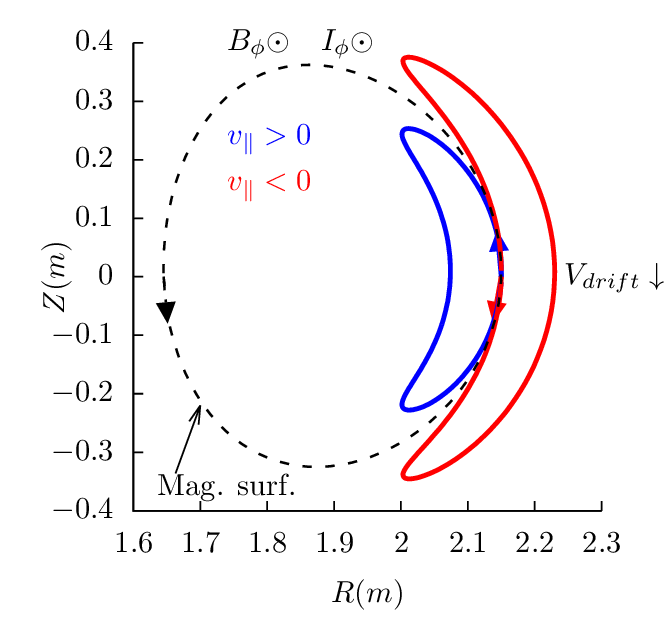
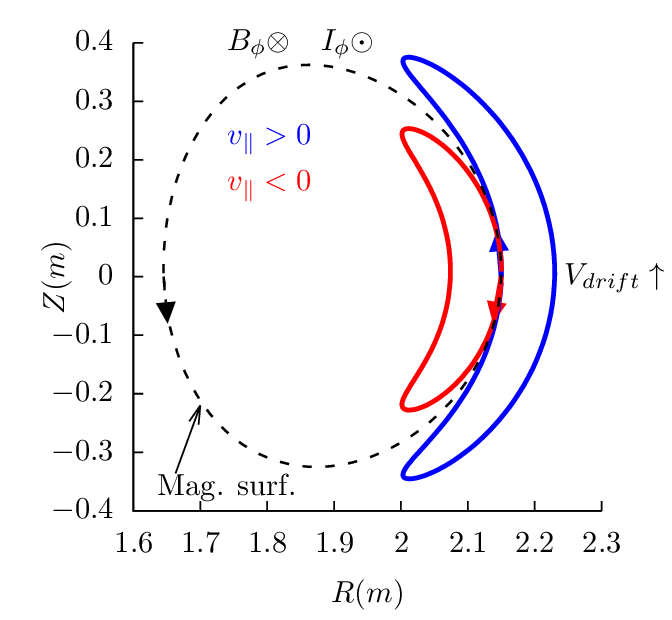
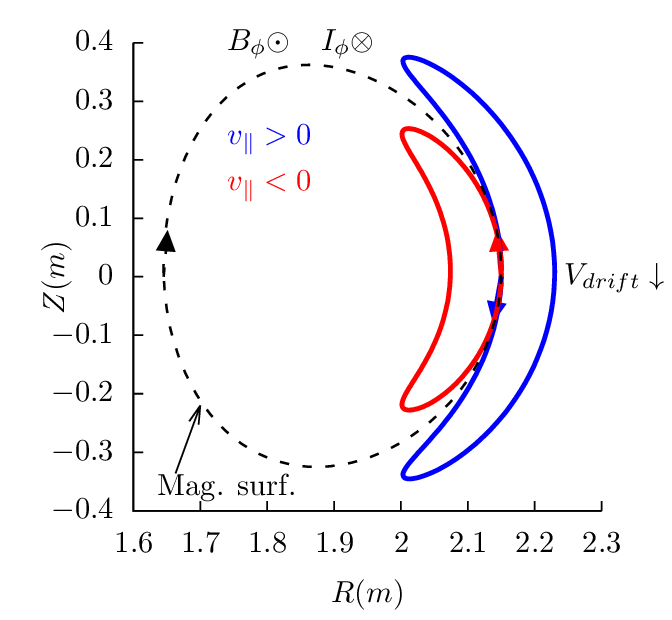
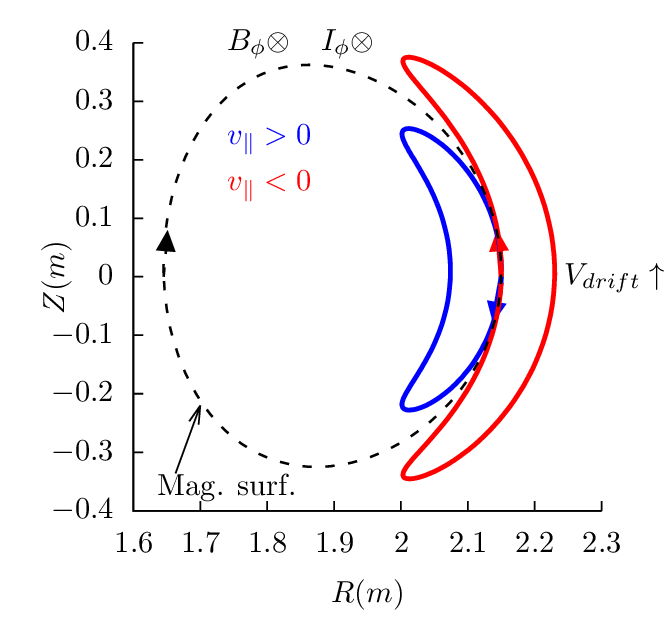
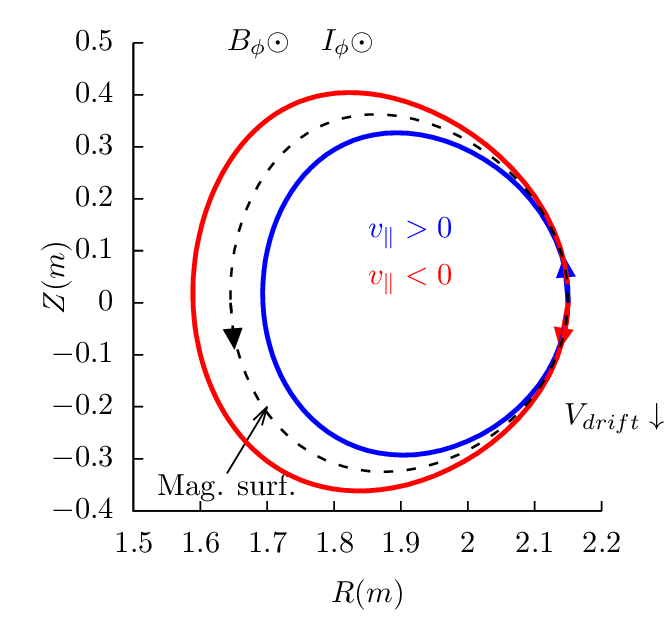
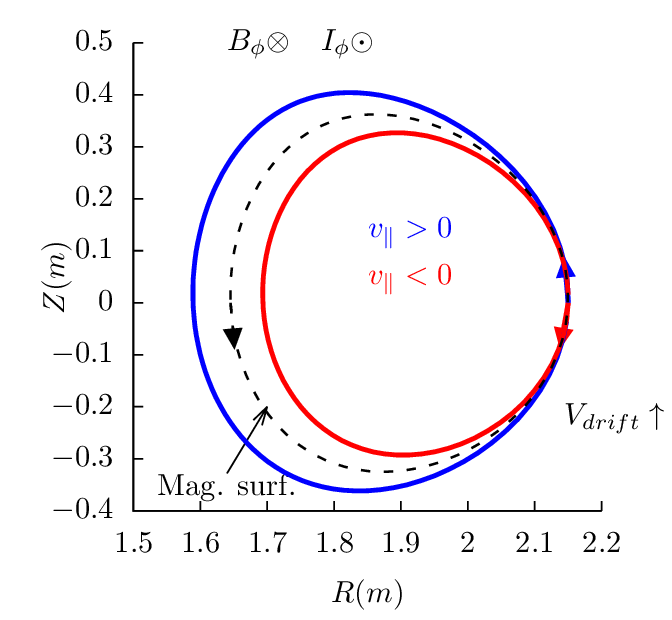
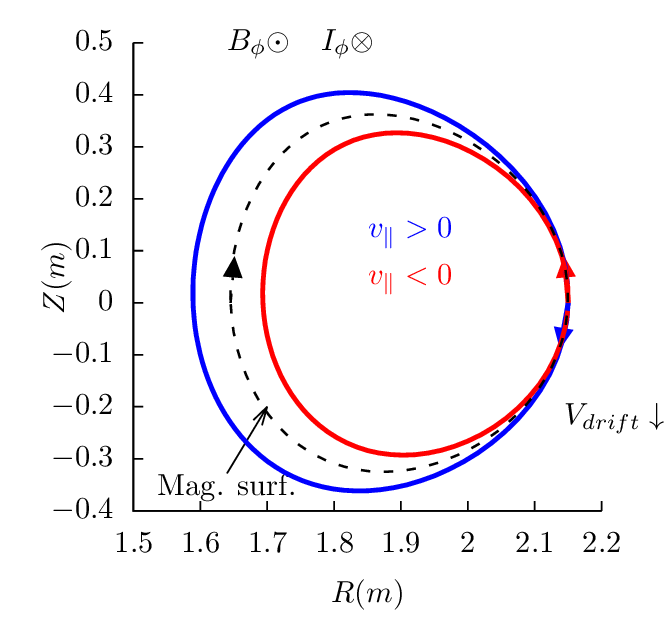
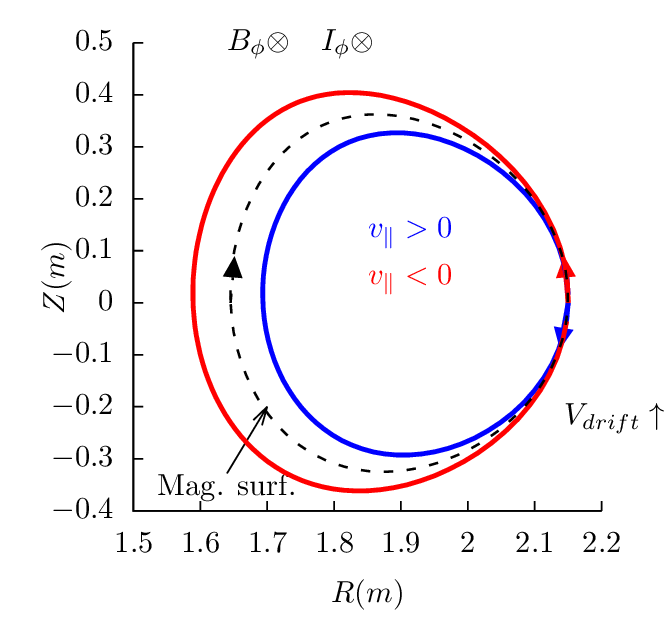
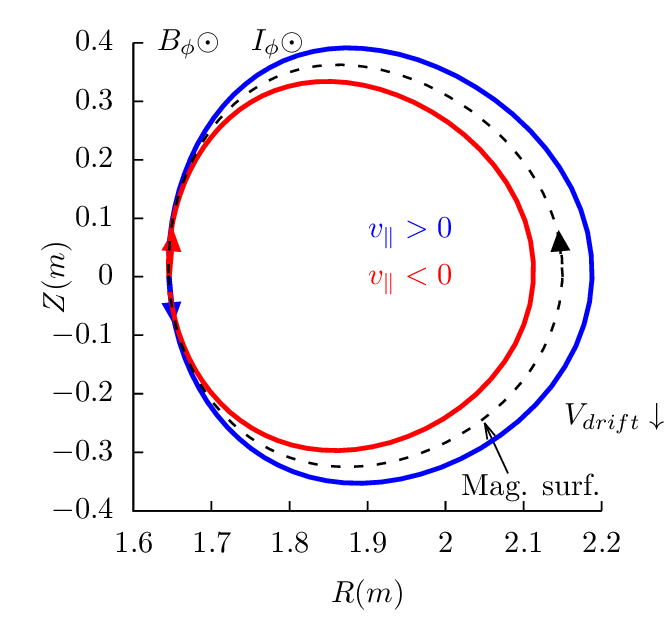
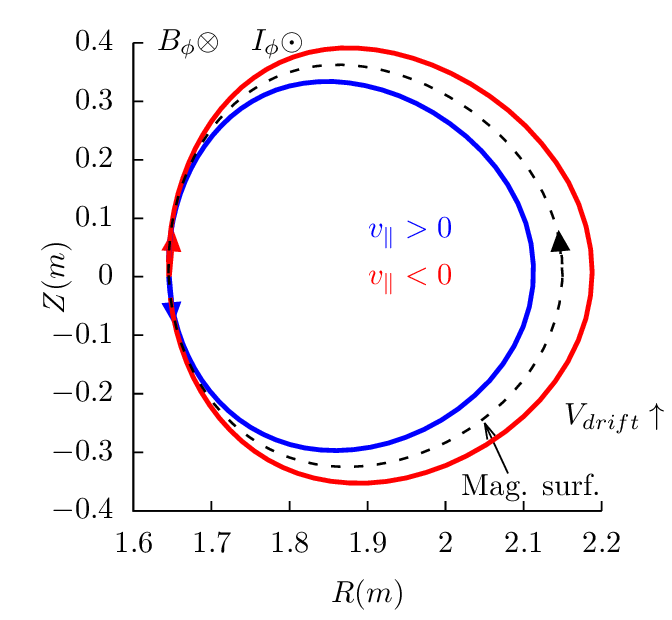
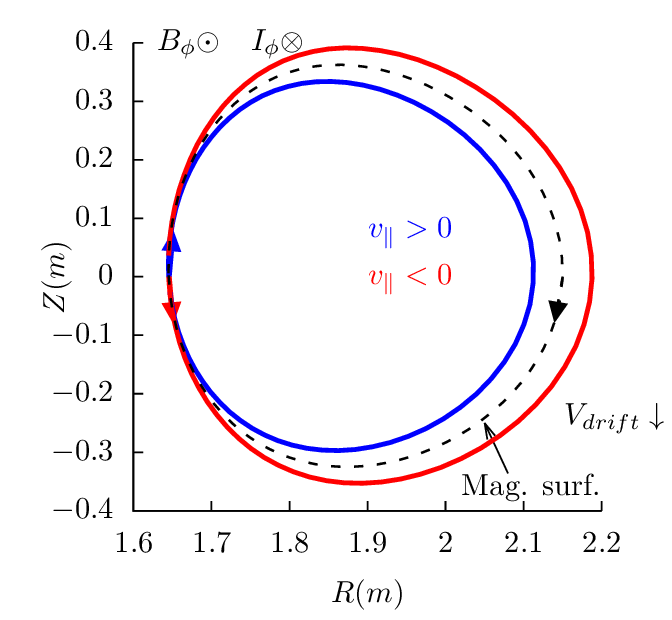
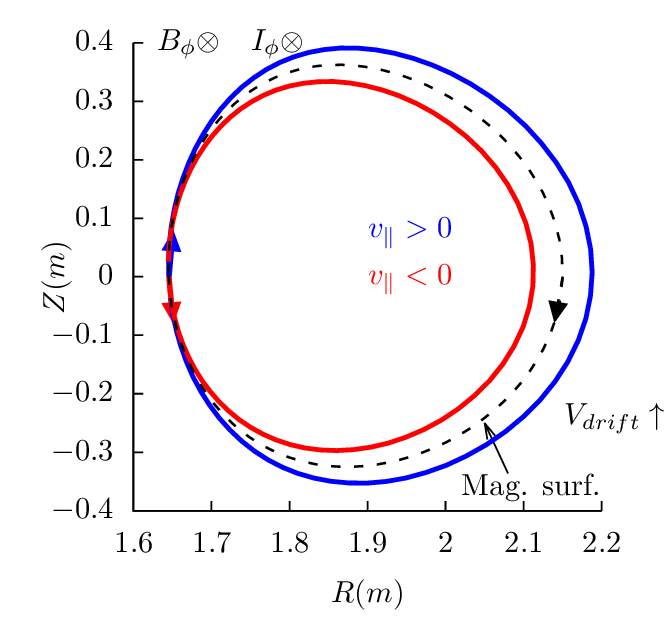
surface. Figures 17-19 plots the drift orbits for all the possible combinitions of tokamak
magnetic configurations and particle initial conditions (assume particles of positive charge, i.e.,
Z∕|Z| > 0).
B×∇B and curvature
drift) is approximatedly vertical, which can be either up or down, depending on the charge sign and
direction of the toroidal magnetic field. Finally, by imposing the magnetic drift on the zero-width orbit,
we can determine whether the guiding center will drift inward or outward from the local magnetic
surface. Figures 17-19 plots the drift orbits for all the possible combinitions of tokamak
magnetic configurations and particle initial conditions (assume particles of positive charge, i.e.,
Z∕|Z| > 0).
Figure 17 can be used to identify the direction of the bootstrap current due to the radial density
gradient of trapped particles. Examining all the cases in Fig. 17, one finds that the boostrap current is
always along the direction of plasma current, and the bootstrapt current direction is independent of the
charge sign.
Next, consider passing particles launched from the low-field-side midplane. Figure 18 plots all the 4
possible cases.
Next, consier a particle launched from the high field side midplane, which must be a passing
particle. Figure 19 plots all the 4 possible cases.
Examining the above results, one finds that reversing the direction of the toroidal magnetic field
does not change the projection of orbits on the poloidal plane, i.e., the location and shape of the
poloidal orbits remain the same. However the direction of the poloidal motion is changed from
clockwise (anti-clockwise) to anti-clockwise (clockwise). (This is because v∥ of a particle
changes sign when the toroidal field is reversed and thus the direction of the poloidal motion
changes).
Examining the above results, we can also find that, for particles launched from low-field-side
midplane, co-current partilces have their orbits inside the magnetic surface at which the
particle is iniitally located, and counter-current particles have thier orbits outside of the
magnetic surface. For particles launched from the high-field-side midplane, the conclusion is
reversed, i.e., co-current partilces have their orbits outside the magnetic surface where they
are initally located, and counter-current particles have thier orbits inside of the magnetic
surface.
These conclusions have important implications for the neutral beam injection, where orbits outside
a reference magnetic surface (birth location) are more likely to be lost to the wall of the
machine. If the neutral beam injection (NBI) is along the same direction of the plasma current,
it is called the co-current injection. Otherwise it is called the counter-current injection.
Using the above conclusions, we know that, for co-current injection, ions ionized at the
low-field-side have better confinement compared with those ionized at the high-field-side. For the
counter-current injection, ions ionized at the high-field-side have better confinement compared with
those ionized at the low-field-side. Whether the overall confinment of ions due to co-current
injection is better or worse than that of the counter-current injection depends on the ratio of
number of ions deposited at the low-field-side to that deposited at the high-field side. For the
shine-through loss to be small, most neutral must ionize at the low-field-side (most neutrals
ionizing at the the high-field side usually means a very high shine-through loss fraction (
>50%)). Therefore, with the assumption that most neutral beam particles are ionized on the
low-field-side, co-curent injection is better than counter-current injection in terms of the first-orbit
loss.
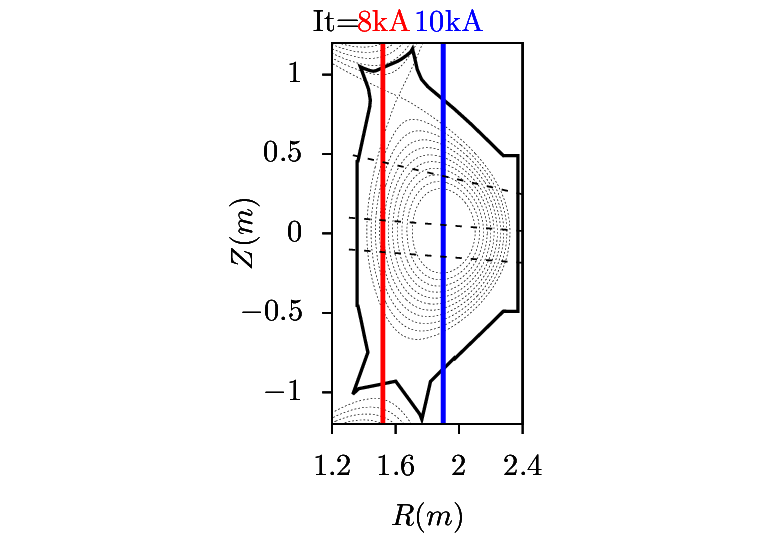
Figure 20 and 21 compares the poloidal orbits of energetic Deuterium particles ionized at the
low-field-side midplane due to co-current and counter-current injection. The results indicate again that
the counter-injected particles ionized at the low-field-side midplane are easy to be lost from the plasma
because their orbits are outside the flux surface where they are ionized, and thus are more likely to
touch the first wall.
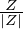 B×∇B and curvature
drift) is approximatedly vertical, which can be either up or down, depending on the charge sign and
direction of the toroidal magnetic field. Finally, by imposing the magnetic drift on the zero-width orbit,
we can determine whether the guiding center will drift inward or outward from the local magnetic
surface. Figures 17-19 plots the drift orbits for all the possible combinitions of tokamak
magnetic configurations and particle initial conditions (assume particles of positive charge, i.e.,
Z∕|Z| > 0).
B×∇B and curvature
drift) is approximatedly vertical, which can be either up or down, depending on the charge sign and
direction of the toroidal magnetic field. Finally, by imposing the magnetic drift on the zero-width orbit,
we can determine whether the guiding center will drift inward or outward from the local magnetic
surface. Figures 17-19 plots the drift orbits for all the possible combinitions of tokamak
magnetic configurations and particle initial conditions (assume particles of positive charge, i.e.,
Z∕|Z| > 0).