5.5 Bounce frequency of barely trapped particles

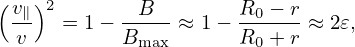
Let us analytically estimate the bounce frequency of barely trapped particles, i.e., particle satisfying the critical condition (76),

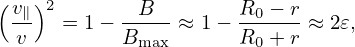(97)

i.e., v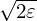_∥ = v, where v_∥ is the parallel velocity on the low-field-side midplane.

The distance along the magnetic field line travelled in half an orbit is about 2πR₀q, then the time needed is then given by

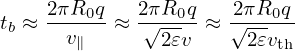(98)

The above approximation is rough since v_∥ changes between zero and 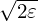v and we still use a constant value, 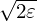v, in approximating it.

Then the bounce (angular) frequency is given by

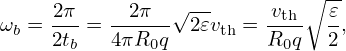(99)

which turns out to be take the same form as Eq. (95). very strange!