The power on a particle is the velocity multiplied by the force, i.e.,
Different order approximations of 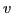 and
and 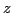 can be used in Eq.
(54) to evaluate the power. If the approximations
can be used in Eq.
(54) to evaluate the power. If the approximations
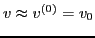 and
and
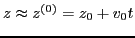 are used, Eq.
(54) is written as
are used, Eq.
(54) is written as
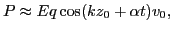 |
(55) |
which is obviously zero when it is averaged over initial position 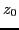 in one
wavelength. If the approximations and
in one
wavelength. If the approximations and
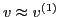 and
and
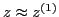 are used, Eq. (54) is written as
are used, Eq. (54) is written as
where, the term proportional to 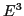 has been neglected. Equation
(56) is identical with Eq. (24). Therefore the
derivation after this point is the same as given in Sec. 2.2.
has been neglected. Equation
(56) is identical with Eq. (24). Therefore the
derivation after this point is the same as given in Sec. 2.2.
yj
2016-01-26