2 Neural network

Neural networks consists of multiple layers of interconnected nodes (neurons), each having a weight for a connection, a bias and activation function. Each layer build upon the previous layer. This progression of computations through the network is called forward propagation. Another process called backpropagation uses algorithms which moves backwards through the layers to efficiently compute the partial derivatives of the loss function with respect to the weights and biases. Combining the forward and backward propagation, we can calculate errors in predictions and then adjusts the weights and biases using the gradient descent method. This process is called training.

2.1 Node (neuron or unit), weight, bias, and activation

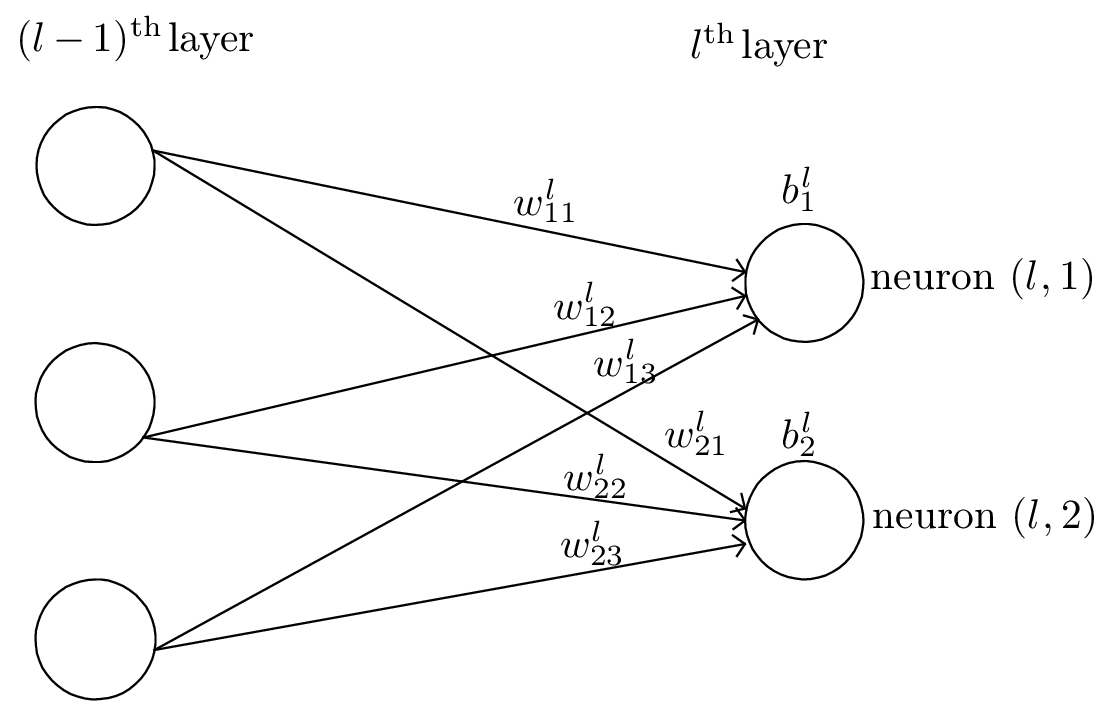
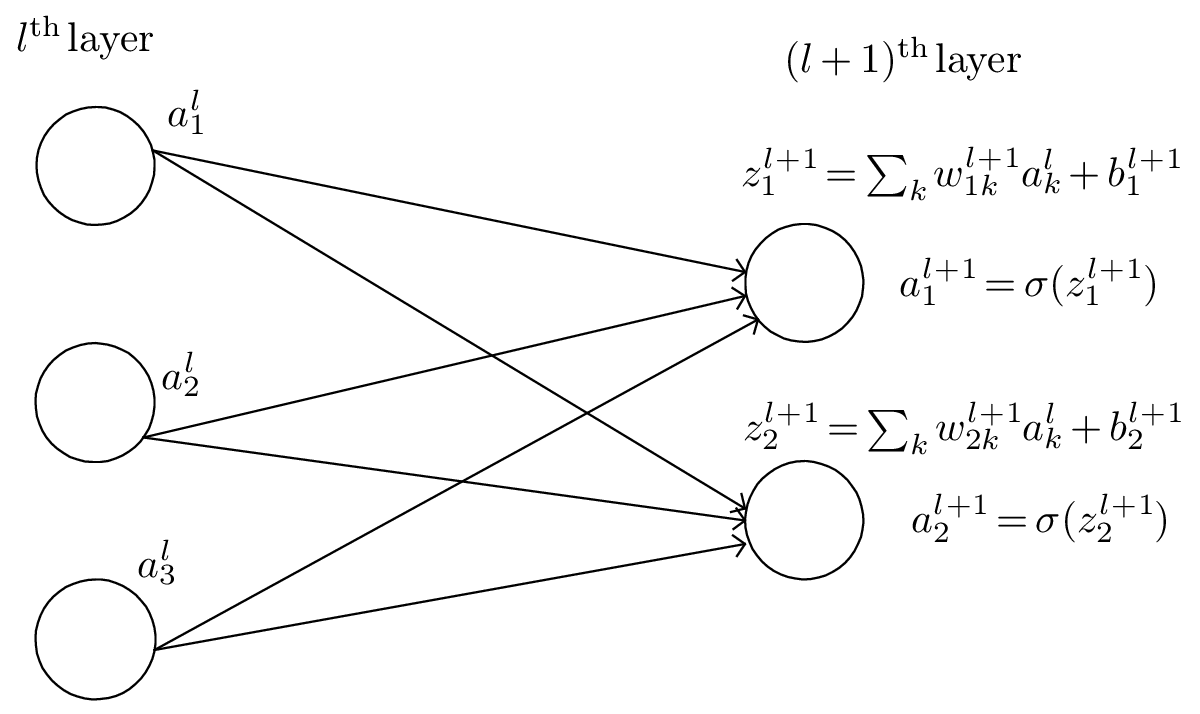
As is shown in Fig. 1, we use w_jk^l to denote the weight for the connection from the k^th neuron in the (l − 1)^th layer to the j^th neuron in the l^th layer. Use b_j^l to denote the bias of the j^th neuron in the l^th layer.

We use a_j^l to denote the output (activation) of the j^th neuron in l^th layer. A neural network model assumes that a_j^l is related to the a^l−1 (output of the previous layer) via

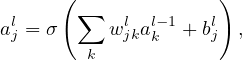(1)

where the summation is over all neurons in the (l − 1)^th layer and σ is a function called activation function which can take various forms, e.g., step function,

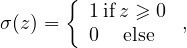(2)

rectified linear unit (ReLU),

(3)

and sigmoid function (“S”-shaped curve, also called logistic function)

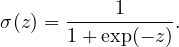(4)

Define z_j^l by

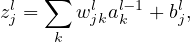(5)

which can be interpreted as an weighted input to the neuron (l,j), then Eq. (1) is written as

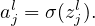(6)

In matrix form, Eq. (5) is written as

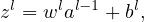(7)

where w^l is a J × K matrix, z^l  and b^l are column vectors of length J, a^l−1 is a column vector of length K, where J and K are the number of neurons in the l^th layer and (l − 1)^th layer, respectively.

The input layer is where data inputs are provided, and the output layer is where the final prediction is made. The input and output layers of a deep neural network are called visible layers. The layers between the input layer and output layer are called hidden layers. Note that the input layer is usually not considered as a layer of the network since it does not involve any computation. In tensorflow, layers refer to the computing layers (i.e., hidden layers and the output layer, not including the input layer). The activation function of each layer can be different. The activation function of the output layer is often chosen as None, ReLU, logistic/tanh, and is usually different from those used in the hidden layers. Here “None” means activation σ(z) = z.

2.2 Loss function

Define a loss (cost, error) function by

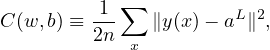(8)

where w and b denotes the collection of all weights and biases in the network, n is the total number of training examples x, the summation is over all the training examples, y(x) is the desired output from the network (i.e., correct answer) when x is the input, and a^L is the actual output from the output layer of the network and is a function of w,b, and x. Note that y and a^L are vectors (with number of elements being the number of neurons in the output layer) and ∥…∥ denotes the vector norm. Explicitly writing out the vector norm, Eq. (8) is written as

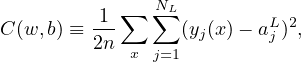(9)

where N_L is the number of neurons in the output layer.

The cost function is the average error of the approximate solution away from the desired exact solution. So the goal of a learning algorithm is to find weights and biases that minimize the cost function. To minimize the cost function over (w,b) using the gradient descent method, we need to compute the partial derivatives ∂C∕∂w_jk^l and ∂C∕∂b_j^l. Next we will discuss how to compute them.

2.3 Gradients of loss function

Note that the loss function involves an average over all the training examples. Denote the loss function for a specific training example by C_x, i.e.,

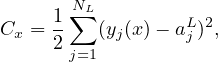(10)

then expression (9) is written as

(11)

Then the partial derivatives ∂C∕∂w_jk^l and ∂C∕∂b_j^l can be written as the sum of ∂C_x∕∂w_jk^l and ∂C_x∕∂b_j^l, i.e.,

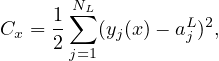(12)

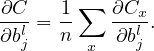(13)

The above formulas indicate that, once ∂C_x∕∂w_jk^l and ∂C_x∕∂b_j^l are known, obtaining  ∂C∕∂w_jk^l and ∂C∕∂b_j^l is trivial, i.e., just averaging them. Therefore, we will focus on C_x (i.e., the cost function for a fixed training example) and discuss how to compute ∂C_x∕∂w_jk^l and ∂C_x∕∂b_j^l.

In practice, we do not sum over all the training examples. Instead, we average the derivative over a small number (say 16) of training examples (a mini batch) and use these approximate derivatives to advance a step. For the next step, we stochastically change to using a different mini batch. This is called stochastic gradient descent (SGD) method.

2.4 Back-propagating algorithm

The cost function C_x is a function of weights and biases of all neurons (the input x and output y(x) are fixed parameters). For a specific neuron (l,j), its weights and biases enter C_x via the combination z_j^l = ∑ _kw_jk^la_k^l−1 + b_j^l. Then it is useful to define the following partial derivative:

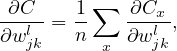(14)

where the partial derivative are taken with fixed weights and biases for all neurons except neuron (l,j). Note that the a_k^l−1 appearing in the expression of z_j^l does not depend on w_jk^l or b_j^l. It only depends on the weights and biases in the layers ≤ (l − 1), which are all fixed when taking the derivative in expression (14). δ_j^l defined in expression (14) is often called the error of neuron (l,j).

Using the chain rule,  ∂C_x∕∂w_jk^l and ∂C_x∕∂b_j^l can be expressed in terms of δ_j^l:

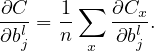(15)

and

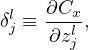(16)

Therefore, if δ_j^l is known, it is trivial to compute the gradients needed in the gradient descent method.

For the output layer (L^th layer), δ_j^l defined in Eq. (14) is written as

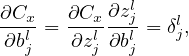(17)

The dependence of C_x on a_j^L is explicitly given by Eq. (10), from which the above expression for δ_j^L is written as

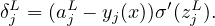(18)

Therefore δ_j^L is easy to compute.

Backpropagation is a way of computing δ_j^l for every layer using recurrence relations: the relation between δ^l and δ^l+1. Noting how the error is propagating through the network, we know the following identity:

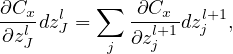(19)

with

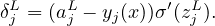(20)

i.e.,

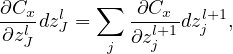(21)

Therefore

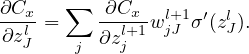(22)

i.e.,

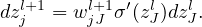(23)

Equation (23) gives the recurrence relations of computing δ^l from δ^l+1. This is called the backpropagation algorithm. Eq. (23) can be written in the matrix form:

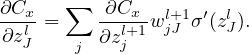(24)

where T stands for matrix transpose, ⊙ is the element-wise product.