The time evolution of the fluid velocity
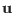 is governed by the
momentum equation
is governed by the
momentum equation
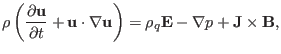 |
(1) |
where 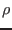 ,
, 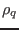 ,
, 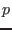 ,
,
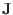 ,
,
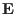 , and
, and
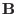 are
mass density, charge density, thermal pressure, current density, electric
field, and magnetic field, respectively. The time evolution of the mass
density
are
mass density, charge density, thermal pressure, current density, electric
field, and magnetic field, respectively. The time evolution of the mass
density 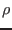 is governed by the mass continuity equation
is governed by the mass continuity equation
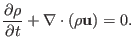 |
(2) |
The time evolution equation for pressure 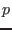 is given by the equation of state
is given by the equation of state
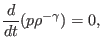 |
(3) |
where 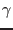 is the ratio of specific heats. The time evolution of
is the ratio of specific heats. The time evolution of
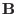 is given by Faraday's law
is given by Faraday's law
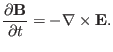 |
(4) |
The current density
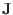 can be considered as a derived quantity,
which is defined through Ampere's law (the displacement current being ignored)
can be considered as a derived quantity,
which is defined through Ampere's law (the displacement current being ignored)
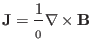 |
(5) |
The electric field
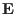 is considered to be a derived quantity, which
is defined through Ohm's law
is considered to be a derived quantity, which
is defined through Ohm's law
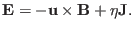 |
(6) |
The charge density 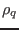 can be considered to be a derived quantity, which
is defined through Poisson's equation,
can be considered to be a derived quantity, which
is defined through Poisson's equation,
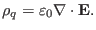 |
(7) |
The above equations constitute a closed set of equations for the time
evolution of four quantities, namely,
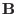 ,
,
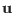 ,
, 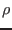 , and
, and
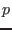 (the electric field
(the electric field
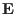 , current density
, current density
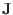 , and
charge density
, and
charge density 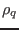 are eliminated by using Eqs. (5),
(6), and (6)). In addition, there is an equation
governing the spatial structure of the magnetic field, namely
are eliminated by using Eqs. (5),
(6), and (6)). In addition, there is an equation
governing the spatial structure of the magnetic field, namely
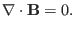 |
(8) |
In summary, the MHD equations can be categorized into three groups of
equations, namely[1],
- Evolution equations for base quantities
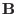 ,
,
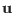 ,
,
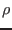 , and
, and 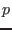 :
:
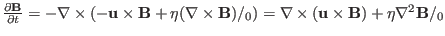
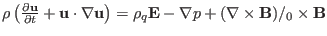
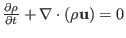 ,
,
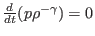 ,
,
- Equation of constraint:
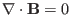 .
.
- Definitions: (i.e., they are considered to be derived quantities.)
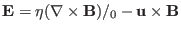 ,
,
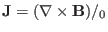 ,
,
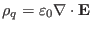 .
.
The electrical field term
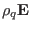 in the momentum equation
(1) is usually neglected because this term is usually much
smaller than other terms for low-frequency phenomena in tokamak plasmas.
in the momentum equation
(1) is usually neglected because this term is usually much
smaller than other terms for low-frequency phenomena in tokamak plasmas.
Subsections
yj
2015-09-04
![]() is governed by the
momentum equation
is governed by the
momentum equation
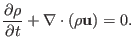
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.