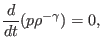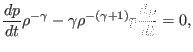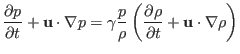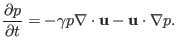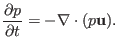The equation of state (3) involves three physical quantities,
namely 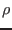 ,
, 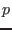 , and
, and
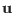 . It turns out that the continuity
equation can be used in the equation to eliminate
. It turns out that the continuity
equation can be used in the equation to eliminate 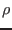 . The equation of
state
. The equation of
state
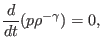 |
(13) |
can be written as
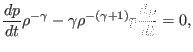 |
(14) |
which simplifies to
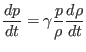 |
(15) |
Expand the total derivative, giving
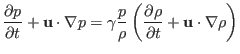 |
(16) |
Using the mass continuity equation to eliminate 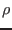 in the above equation
gives
in the above equation
gives
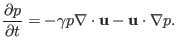 |
(17) |
This equation governs the time evolution of the pressure. A way to memorize
this equation is that, if
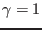 , the equation will take the same form
as a continuity equation, i.e.,
, the equation will take the same form
as a continuity equation, i.e.,
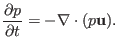 |
(18) |
yj
2015-09-04
![]() ,
, ![]() , and
, and
![]() . It turns out that the continuity
equation can be used in the equation to eliminate
. It turns out that the continuity
equation can be used in the equation to eliminate ![]() . The equation of
state
. The equation of
state