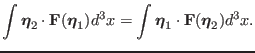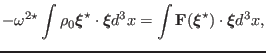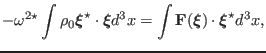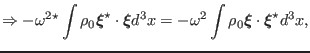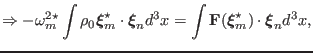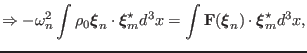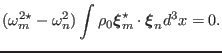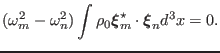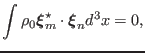Using Eqs. (36) and (37) to eliminate 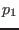 and
and
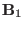 from Eq. (35), we obtain
from Eq. (35), we obtain
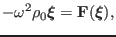 |
(47) |
where
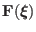 , the linear force operator, is given by
, the linear force operator, is given by
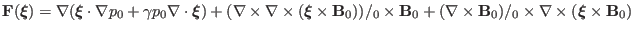 |
(48) |
It can be proved that the linear force operator
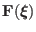 is self-adjoint (or Hermitian) (I have not proven this), i.e., for any two
functions
is self-adjoint (or Hermitian) (I have not proven this), i.e., for any two
functions
 and
and
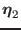 that satisfy the same
boundary condition, we have
that satisfy the same
boundary condition, we have
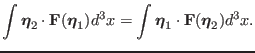 |
(49) |
As a consequence of the self-adjointness, the eigenvalue, 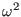 , must be
a real number, which implies that
, must be
a real number, which implies that 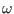 itself is either purely real or
purely imaginary. [Proof: Taking the complex conjugate of Eq. (47),
we obtain
itself is either purely real or
purely imaginary. [Proof: Taking the complex conjugate of Eq. (47),
we obtain
![$\displaystyle - \rho_0 (\omega^2 \ensuremath{\boldsymbol{\xi}})^{\star} = [\mathbf{F}(\ensuremath{\boldsymbol{\xi}})]^{\star} .$](img170.png) |
(50) |
Note that the expression of
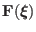 given in Eq.
(48) have the property
given in Eq.
(48) have the property
![$ [\mathbf{F}(\ensuremath{\boldsymbol{\xi}})]^{\star}
=\mathbf{F} (\ensuremath{\boldsymbol{\xi}}^{\star})$](img171.png) , Using this, equation (50) is
written
, Using this, equation (50) is
written
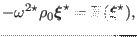 |
(51) |
Taking the scalar product of both sides of the above equation with
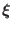 and integrating over the entire volume of the system, gives
and integrating over the entire volume of the system, gives
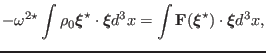 |
(52) |
Using the self-ajointness of
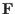 , the above equation is written
, the above equation is written
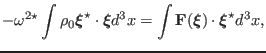 |
(53) |
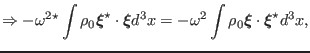 |
(54) |
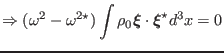 |
(55) |
Since
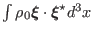 is
non-zero for any non-trivial eigenfunction, it follows from Eq.
(55) that
is
non-zero for any non-trivial eigenfunction, it follows from Eq.
(55) that
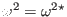 , i.e.,
, i.e., 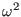 must be a
real number, which implies that
must be a
real number, which implies that 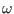 is either purely real or purely
imaginary.] It can also be proved that two eigenfunctions with different
is either purely real or purely
imaginary.] It can also be proved that two eigenfunctions with different
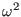 are orthogonal to each other. [Proof:
are orthogonal to each other. [Proof:
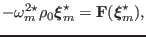 |
(56) |
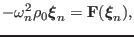 |
(57) |
Taking the scalar product of both sides of Eq. (56) with
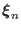 and integrating over the entire volume of the system, gives
and integrating over the entire volume of the system, gives
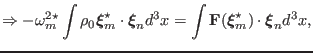 |
(58) |
Taking the scalar product of both sides of Eq. (57) with
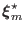 and integrating over the entire volume of the
system, gives
and integrating over the entire volume of the
system, gives
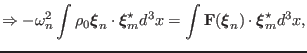 |
(59) |
Combining the above two equations, we obtain
Using the self-ajointness of
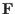 , we know the right-hand side of Eq.
(60) is zero. Thus Eq. (60) is written
, we know the right-hand side of Eq.
(60) is zero. Thus Eq. (60) is written
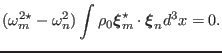 |
(61) |
Using
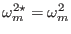 , the above equation is written
, the above equation is written
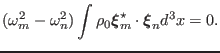 |
(62) |
Since we assume
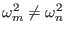 , the above equation reduces to
, the above equation reduces to
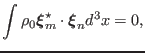 |
(63) |
i.e.,
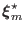 and
and
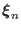 are orthogonal to each
other.]
are orthogonal to each
other.]
yj
2015-09-04
![]() and
and
![]() from Eq. (35), we obtain
from Eq. (35), we obtain