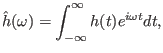A general perturbation can be written
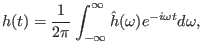 |
(31) |
where the coefficient
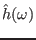 is given by the Fourier
transformation of
is given by the Fourier
transformation of 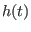 , i.e.,
, i.e.,
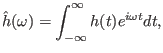 |
(32) |
Using the definition of the Fourier transformtion, it is ready to prove that
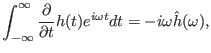 |
(33) |
and
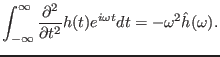 |
(34) |
Performing Fourier transformation (in time) on both sides of the the
linearized momentum equation (30) and noting that the equilibrium
quantities are all independent of time, we obtain
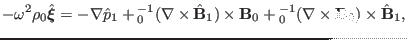 |
(35) |
where use has been made of the property in Eq. (34). Similarly, the
Fourier transformation of the equations of state (29) is written
 |
(36) |
and the Fourier transformation of Faraday's law (28) is written
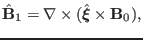 |
(37) |
Equations (35)-(37) agree with Eqs. (12)-(14) in Cheng's
paper[3]. They constitute a closed set of equations for
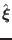 ,
,
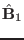 , and
, and 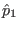 . In the next
section, for notation ease, the hat on
. In the next
section, for notation ease, the hat on
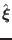 ,
,
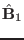 , and
, and 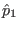 will be omitted, with the understanding
that they are the Fourier transformations of the corresponding quantities.
will be omitted, with the understanding
that they are the Fourier transformations of the corresponding quantities.
yj
2015-09-04