Next: Plasma displacement vector Up: Notes on linear ideal Previous: Summary of resistive MHD
Next, consider the linearized version of the ideal MHD equations. Use
![]() ,
,
![]() ,
, ![]() , and
, and ![]() to denote the equilibrium
fluid velocity, magnetic field, plasma pressure, and mass density,
respectively. Use
to denote the equilibrium
fluid velocity, magnetic field, plasma pressure, and mass density,
respectively. Use
![]() ,
,
![]() ,
, ![]() , and
, and ![]() to
denote the perturbed fluid velocity, magnetic field, plasma pressure, and mass
density, respectively. Consider only the case that there is no equilibrium
flow, i.e.,
to
denote the perturbed fluid velocity, magnetic field, plasma pressure, and mass
density, respectively. Consider only the case that there is no equilibrium
flow, i.e.,
![]() . From Eq. (21), the linearized
equation for the time evolution of the perturbed pressure is written as
. From Eq. (21), the linearized
equation for the time evolution of the perturbed pressure is written as
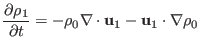 |
(26) |