The induction equation is given by Eq. (37), i.e.,
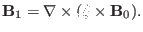 |
(68) |
Next, consider the
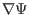 component of the above equation. Taking
scalar product of the above equation with
component of the above equation. Taking
scalar product of the above equation with
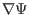 , we obtain
, we obtain
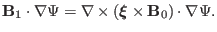 |
(69) |
![$\displaystyle \Rightarrow Q_{\psi} = \nabla \times \left[ \frac{\xi_{\psi}}{\ve...
...(\mathbf{B}_0 \times \nabla \Psi) \times \mathbf{B}_0 \right] \cdot \nabla \Psi$](img205.png) |
(70) |
![$\displaystyle \Rightarrow Q_{\psi} = \nabla \times \left[ \frac{\xi_{\psi}}{\ve...
...} \nabla \Psi \times \mathbf{B}_0 + \xi_s \nabla \Psi \right] \cdot \nabla \Psi$](img206.png) |
(71) |
![$\displaystyle \Rightarrow Q_{\psi} = \left[ \nabla \times \left( \frac{\xi_{\ps...
...thbf{B}_0 \right) + \nabla \times (\xi_s \nabla \Psi) \right] \cdot \nabla \Psi$](img207.png) |
(72) |
![$\displaystyle \Rightarrow Q_{\psi} = \left[ \nabla \times \left( \frac{\xi_{\ps...
...mathbf{B}_0 \right) + \nabla \xi_s \times \nabla \Psi \right] \cdot \nabla \Psi$](img208.png) |
(73) |
![$\displaystyle \Rightarrow Q_{\psi} = \left[ \nabla \times \left( \frac{\xi_{\ps...
...\Psi \vert^2} \nabla \Psi \times \mathbf{B}_0 \right) \right] \cdot \nabla \Psi$](img209.png) |
(74) |
![$\displaystyle \Rightarrow Q_{\psi} = \left[ (\mathbf{B}_0 \cdot \nabla) \left( ...
...a \Psi \vert^2} \nabla \Psi \cdot \nabla \mathbf{B}_0 \right] \cdot \nabla \Psi$](img210.png) |
(75) |
![$\displaystyle Q_{\psi} = \left[ \frac{\xi_{\psi}}{\vert \nabla \Psi \vert^2} (\...
...a \Psi \vert^2} \nabla \Psi \cdot \nabla \mathbf{B}_0 \right] \cdot \nabla \Psi$](img211.png) |
(76) |
![$\displaystyle Q_{\psi} = \left[ \frac{\xi_{\psi}}{\vert \nabla \Psi \vert^2} (\...
...a \Psi \vert^2} \nabla \Psi \cdot \nabla \mathbf{B}_0 \right] \cdot \nabla \Psi$](img211.png) |
(77) |
![$\displaystyle Q_{\psi} = \left[ \frac{\xi_{\psi}}{\vert \nabla \Psi \vert^2} (\...
...\Psi \vert^2} (\nabla \Psi \cdot \nabla \mathbf{B}_0) \cdot \nabla \Psi \right]$](img212.png) |
(78) |
Excluding
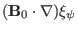 terms, the terms on the
right hand side (r.h.s) of the above equation can be written
terms, the terms on the
right hand side (r.h.s) of the above equation can be written
Using
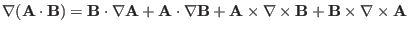 , we obtain
, we obtain
| 0 |
 |
![$\displaystyle \nabla \Psi \cdot \nabla (\nabla \Psi \cdot \mathbf{B}_0) = \nabl...
...[\mathbf{B}_0 \cdot \nabla \nabla \Psi + \nabla \Psi \cdot \nabla
\mathbf{B}_0]$](img221.png) |
(81) |
The r.h.s of the above equation is exactly the term appearing on the
right-hand side of Eq. (79). Thus we obtain
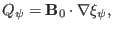 |
(82) |
which agrees with Eq. (20) in Cheng's paper[3].
yj
2015-09-04
![$\displaystyle \Rightarrow Q_{\psi} = \nabla \times \left[ \frac{\xi_{\psi}}{\ve...
...(\mathbf{B}_0 \times \nabla \Psi) \times \mathbf{B}_0 \right] \cdot \nabla \Psi$](img205.png)
![$\displaystyle \Rightarrow Q_{\psi} = \nabla \times \left[ \frac{\xi_{\psi}}{\ve...
...} \nabla \Psi \times \mathbf{B}_0 + \xi_s \nabla \Psi \right] \cdot \nabla \Psi$](img206.png)
![$\displaystyle \Rightarrow Q_{\psi} = \left[ \nabla \times \left( \frac{\xi_{\ps...
...thbf{B}_0 \right) + \nabla \times (\xi_s \nabla \Psi) \right] \cdot \nabla \Psi$](img207.png)
![$\displaystyle \Rightarrow Q_{\psi} = \left[ \nabla \times \left( \frac{\xi_{\ps...
...mathbf{B}_0 \right) + \nabla \xi_s \times \nabla \Psi \right] \cdot \nabla \Psi$](img208.png)
![$\displaystyle \Rightarrow Q_{\psi} = \left[ \nabla \times \left( \frac{\xi_{\ps...
...\Psi \vert^2} \nabla \Psi \times \mathbf{B}_0 \right) \right] \cdot \nabla \Psi$](img209.png)
![$\displaystyle \Rightarrow Q_{\psi} = \left[ (\mathbf{B}_0 \cdot \nabla) \left( ...
...a \Psi \vert^2} \nabla \Psi \cdot \nabla \mathbf{B}_0 \right] \cdot \nabla \Psi$](img210.png)
![$\displaystyle Q_{\psi} = \left[ \frac{\xi_{\psi}}{\vert \nabla \Psi \vert^2} (\...
...a \Psi \vert^2} \nabla \Psi \cdot \nabla \mathbf{B}_0 \right] \cdot \nabla \Psi$](img211.png)
![$\displaystyle Q_{\psi} = \left[ \frac{\xi_{\psi}}{\vert \nabla \Psi \vert^2} (\...
...a \Psi \vert^2} \nabla \Psi \cdot \nabla \mathbf{B}_0 \right] \cdot \nabla \Psi$](img211.png)
![$\displaystyle Q_{\psi} = \left[ \frac{\xi_{\psi}}{\vert \nabla \Psi \vert^2} (\...
...\Psi \vert^2} (\nabla \Psi \cdot \nabla \mathbf{B}_0) \cdot \nabla \Psi \right]$](img212.png)