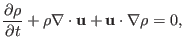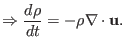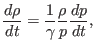The continuity equation can be written
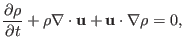 |
(368) |
which can be further written
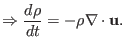 |
(369) |
Then the incompressible condition
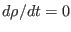 reduces to that
reduces to that
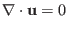 |
(370) |
On the other hand, equation (15) indicates that
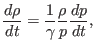 |
(371) |
which indicates that for incompressible plasma
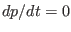 .
.
yj
2015-09-04