Next: Fourier transformation in time Up: Linearized ideal MHD equation Previous: Linearized ideal MHD equation
In dealing with the linear case of MHD theory, it is convenient to introduce
the plasma displacement vector
![]() , which is defined through the
following equation
, which is defined through the
following equation
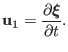 |
(27) |
yj 2015-09-04