[next] [tail] [up]

5.1 Eliminate ∂⟨δϕ⟩α∕∂t term on the right-hand side of Eq. (133)

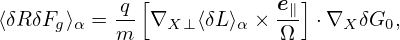
Note that the coefficient before ∂F0∕∂𝜀 in Eq. (133) involves the time derivative of ⟨δϕ⟩α, which is problematic if treated by using explicit finite difference in particle simulations (I test the algorithm that treats this term by implicit scheme, the result roughly agrees with the standard method discussed in Sec. 5.6). It turns out that ∂⟨δΦ⟩α∕∂t can be eliminated by defining another gyro-phase independent function δf by

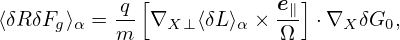q ∂F δf = --⟨δΦ ⟩α --0-+δG0. m ∂𝜀
(135)

Then, in terms of δf, the perturbed distribution function δF is written as

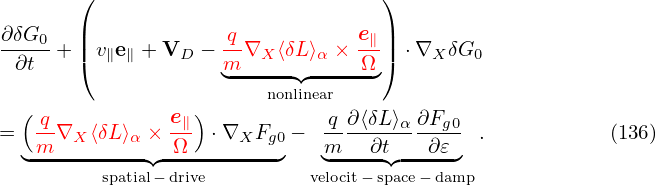δF = q-(δΦ − ⟨δΦ ⟩α )∂F0+ δf. m ∂𝜀
(136)

Using Eq. (135) and Eq. (133), the equation for δf is written as

[ ∂ ] ∂t + (v∥e∥ + VD + δVD )⋅∇X δf [ ] − q-∂F0- ∂-+ (v∥e∥ + VD + δVD )⋅∇X ⟨δϕ⟩α m ∂ 𝜀 ∂[t ] − q-⟨δϕ⟩ ∂-+ (v e + V + δV )⋅∇ ∂F0- m α ∂t ∥ ∥ D D X ∂ 𝜀 q ∂⟨δL ⟩α ∂F0 = − δVD ⋅∇XF0 − m- --∂t---∂𝜀- (137)
Noting that ∂F0∕∂t = 0, e∥⋅∇F0 = 0, ∇F0 ∼ O(λ1)F0, we find that the third line of the above equation is of order O(λ3) and thus can be dropped. Moving the second line to the right-hand side and noting that ⟨δL⟩α = ⟨δϕ − v ⋅ δA⟩α, the above equation is written as
[ ] -∂ + (ve + V + δV )⋅∇ δf ∂t ∥ ∥ D D X = − δVD ⋅∇XF0 q [ ∂⟨v⋅δA ⟩α ] ∂F0 − m- − ---∂t----− (v∥e∥ + VD + δVD )⋅∇X ⟨δΦ⟩α ∂𝜀-, (138)
where two ∂⟨ϕ⟩α∕∂t terms cancel each other. Note that the right-hand side of Eq. (138) contains a nonlinear term δVD ⋅∇X⟨δΦ⟩α. This is different from the original Frieman-Chen equation, where all nonlinear terms appear on the left-hand side. [Equation (138) corresponds to Eq. (A8) in Yang Chen’s paper[2] (where the first minus on the right-hand side is wrong and should be replaced with q∕m; one q is missing before ∂(v ⋅ δA)∕∂t in A9).]

The blue term in expression (136) gives “the polarization density” when integrated in the velocity space (discussed in Sec. 5.6). The reason for the name “polarization” is that (δΦ −⟨δΦ⟩α) is the difference between the local value and the averaged value on a gyro-ring, expressing a kind of “separation”.

[next] [front] [up]