[next] [prev] [prev-tail] [tail] [up]

5 Parallel Ampere’s Law

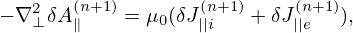
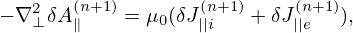− ∇2⊥ δA(∥n+1)= μ0(δJ (n||i+1)+ δJ(|n|e+1)),
(215)

where the parallel currents are given by

∫ q2 ∂F δJ(n||i+1)= δJ|′|i(δϕ(n),δA(∥n)) + (v(∥n+1))2-i-⟨δA (n∥+1)⟩α--i0dv, mi ∂𝜀
(216)

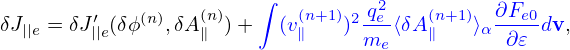∫ ′ (n) (n) (n+1) 2 q2e (n+1) ∂Fe0 δJ||e = δJ||e(δϕ ,δA ∥ )+ (v∥ ) me⟨δA ∥ ⟩α ∂𝜀 dv,
(217)

where δJ∥i′ and δJ∥e′ is the parallel current carried by the distribution function δh in Eq. (203), which are updated from the value at the nth time step to the (n + 1)th time step using an explicit scheme and therefore does not depends on the field at the (n + 1)th step. The blue terms  in Eqs. (216) and (217) are sometimes called “skin current”, which depend on the unknown field at the (n + 1)th step and thus need to be moved to the left-hand side of Ampere’s law (215) if we want to solve this equation by direct methods. In this case, equation (215) is written as

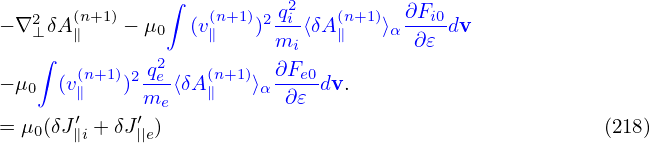
∫ − ∇2 δA (n+1)− μ (v(n+1))2 q2i-⟨δA (n+1)⟩ ∂Fi0dv ⊥ ∥ 0 ∥ mi ∥ α ∂𝜀 ∫ (n+1)2 q2e (n+1) ∂Fe0 − μ0 (v∥ ) me-⟨δA ∥ ⟩α-∂𝜀-dv. = μ (δJ′ +δJ ′) (218) 0 ∥i ||e
Then we need to put the blue terms into matrix form. If we put the bule terms into martrix form by using numerical spatial grid integration (as we do for the polarization density), then there arises the cancellation propblem (i.e., the two parts of the distribution are evaluated by different methods,one is grid-based and the other is MC marker based, there is a risk that the sum of the two terms will be inaccurate when the two terms are of opposite signs and large amplitudes, and the final result amplitude is expected to be much smaller than the amplituded of the two terms). If we get the matrix form by evaluating it numerically using MC markers (which can avoid the cancellation problem), the corresponding matrix will depends on markers and thus needs to be re-constructed and inverted each time-step, which is computationally expensive.

Therefore we go back to Eq. (215) and try to solve it using iterative methods. However, it is found numerically that directly using Eq. (215) as an iterative scheme is usually divergent. To obtain a convergent iterative scheme, we need to have an approximate form for the blue terms, which is independent of markers and so that it is easy to construct its matrix, and then subtract this approximate form from both sides. After doing this, the iterative scheme has better chance to be convergent (partially due to that the right-hand side becomes smaller). An approximate form is that derived by neglecting the FLR effect given in Sec. 4.6. Using this, the iterative scheme for solving Eq. (215) is written as

( ω2 ω2 ) − ∇2⊥δA (n∥+1)− −-pi2 δA(∥n+1)−-pe2 δA (n∥+1) c c = μ0(δJ′∥i + δJ′||e) ∫ 2 +μ0 (v(∥n+1))2 qi⟨δA (n∥+1)⟩α ∂Fi0dv ∫ mi ∂𝜀 +μ (v(n+1))2 q2e-⟨δA (n+1)⟩ ∂Fe0dv 0 ∥ me ∥ α ∂𝜀 ( ω2pi (n+1) ω2pe (n+1)) − − -2 δA ∥ − --2 δA ∥ . (219) c c
In the drift-kinetic limit (i.e., neglecting the FLR effect), the blue and red terms on the right-hand side of the above equation cancel each other exactly. Even in this case, it is found numerically that these terms need to be retained and the blue terms are evaluated using markers. Otherwise, numerical inaccuracy can give numerical instabilities, which is the so-called cancellation problem. The explanation for this is as follows. The blue terms are part of the current. The remained part of the current carried by δh is computed by using Monte-Carlo integration over markers. If the blue terms are evaluated analytically, rather than using Monte-Carlo integration over markers, then the cancellation between this analytical part and Monte-Carlo part can have large error (assume that there are two large contribution that have opposite signs in the two parts) because the two parts are evaluated using different methods and thus have different accuracy, which makes the cancellation less accurate.

Because the ion skin current is less than its electron counterpart by a factor of me∕mi, its accuracy is not important. The cancellation error is not a problem and hence can be neglected. In this case, equation (219) is simplified as

( ) 2 (n+1) ω2pi (n+1) ω2pe (n+1) − ∇ ⊥δA ∥ − − c2 δA∥ − c2 δA ∥ ′ ′ = μ0∫(δJ∥i + δJ||e) (n+1)2-qe2 (n+1) ∂Fe0 +μ0 (v∥ ) me ⟨δA∥ ⟩α ∂𝜀 dv ( ω2 ) − − -p2eδA (∥n+1) . (220) c
Note that the blue term will be evaluated using Monte-Carlo markers.

[next] [prev] [prev-tail] [front] [up]