Time evolution of the physical distribution function

4.1 Time evolution of the physical distribution function

4.1.1 Full-f formula

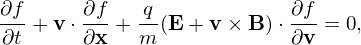
The collisionless kinetic equation (Vlasov equation) is given by

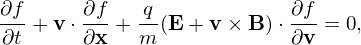∂f-+ v⋅ ∂f-+-q(E + v× B )⋅ ∂f-= 0, ∂t ∂x m ∂v

(59)

It is ready to ﬁnd that the characteristic lines of the equation is given by

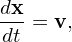dx-= v, dt

(60)

and

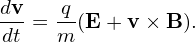dv q ---= -(E + v ×B ). dt m

(61)

Along a characteristic line, the kinetic equation is written

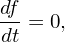df -- = 0, dt

(62)

where f is the total particle distribution function (full-f). Particles methods that use Monte-Carlo sampling to approximate the total f are called total-f or full-f method.

4.1.2 Delta-f formula

Since the phenomena we consider in tokamak plasmas are usually developing from an equilibrium or near-equilibrium state, it is desirable to calculate the the evolution of the only the perturbation, instead of the total f. Therefore, we write f as the sum of a known time-independent distribution function f₀ (∂f₀∕∂t=0) and a unknown time-dependent perturbation δf (∂δf∕∂t≠0):

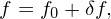f = f0 + δf,

(63)

Then the kinetic equation (62) is written

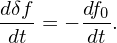dδf df0 -dt-= −-dt .

(64)

Particle methods that use Monte-Carlo sampling to approximate the δf are usually called δf method. When the right-hand side of Eq. (64) is known, Eq. (64) can be integrated to obtain the time evolution of δf. The time evolution of δf can also be obtained by using

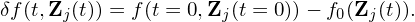δf(t,Z (t)) = f(t = 0,Z (t = 0))− f (Z (t)). j j 0 j

(65)

In this way, the time integration of δf∕dt is avoided, which may reduce the computational overhead and improve the accuracy of δf. This seemingly trivial method was emphasized in a CPC paper[1], which introduces an adaptive f₀ method based on this idea. I have tested this method in my toy code about the 1D Landau damping, which gave the same results as the usual method. However, Yang Chen pointed out that this method is never used in simulations of tokamak plasmas due to the following reasons. The chosen equilibrium distribution function f₀ in tokamak plasmas simulation is usually not a solution the following time-independent Vlasov equation:

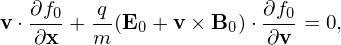v⋅ ∂f0 + q-(E + v × B )⋅ ∂f0= 0, ∂x m 0 0 ∂v

(66)

Instead, the chosen f₀ is a solution of the following equation

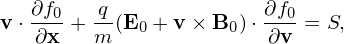v⋅ ∂f0 + q-(E0 + v × B0)⋅ ∂f0= S, ∂x m ∂v

(67)

where S is a nonzero term. On the other hand, the perturbation part is governed by the following equation

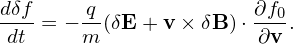dδf q ∂f ----= −--(δE + v× δB )⋅--0. dt m ∂v

(68)

Then it is ready to prove that the actual kinetic equation for the full f in the usual tokamak simulation is actually given by

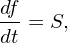df -- = S, dt

(69)

which indicates that f is not a constant along the characteristic curves and thus is not consistent with the algorithm given in Eq. (65). **may be wrong, check**The case given in Eq. (69) is the more relevant case to tokamak experiments where a particular form of f₀ is maintained by external sources and we are asked to calculate the perturbation evolution around f₀.**wrong!

[next] [front] [up]