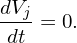
For Hamiltonian motion in particular and non-diffusive motion in general, any particle distribution function g(x,v,t) satisfies that dg∕dt = 0. In other words, the phase-space particle flow is volume preserving (this is Louisville’s theorem), i.e.,
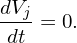 | (70) |
i.e, the phase-space volume sampled by a marker does not change along the characteristic curves. This is good news for PIC simulation because this means that the marker distribution is known exactly along the characteristic line at every time-step and we do not need to numerically evaluate it (numerically evaluating the marker distribution by directly counting markers would be noisy due to the small number of markers loaded and should be avoided in practice whenever possible).
For diffusive motion, the phase space particle flow is usually not volume preserving, i.e.,
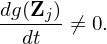 | (71) |
For this case, the values of g at markers need to be evaluated numerically every time step, which is usually noisy and time-consuming in terms of CPU time. Therefore, this kind of evaluation should be avoided in practice whenever possible. The usual way of achieving this is by choosing a suitable initial distribution for the markers, so that g remains approximately constant along the trajectory of markers[3].
The marker distribution chosen in practice is determined by the desired resolution of phase space of interest, not determined by the physical particle distribution, i.e., the initial marker distribution can be different from the physical particle distribution.