2.1 Phase-space sampling and Phase space volume sampled by a marker

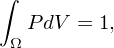
Suppose the phase space Z = (r,v) is described by general curvlinear coordinates (α,β,γ,v_α,v_β,v_γ). Given a probability density function P = P(α,β,γ,v_α,v_β,v_γ) that satisfies the following normalization condition

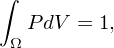(1)

where Ω is the phase space region of interest, dV is the phase-space volume element. In terms of the (α,β,γ,v_α,v_β,v_γ) coordinates, dV is given by dV = |𝒥_r𝒥_v|dαdβdγdv_αdv_βdv_γ, where 𝒥_r is the Jacobian of transformation from Cartesian space coordinates (x,y,z) to curvlinear coordinates (α,β,γ), and 𝒥_v is the Jacobian of transformation from Cartesian velocity coordinates (v_x,v_y,v_z) to curvlinear coordinates (v_α,v_β,v_γ). Using this, the normalization condition (1) is written as

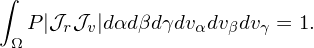(2)

Use this probability density function to sample the phase space region Ω with N markers, then the marker distribution function g is given by

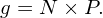(3)

The definition of g implies that the number of markers within a small volume of phase-space dV is given by

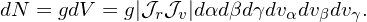(4)

Therefore the average phase space volume occupied (or sampled) by a marker, V _p, is written as

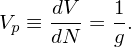(5)

In practical numerical implementation in a curvlinear coordinate system, I prefer to define P′ and g′ by

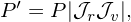(6)

and

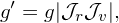(7)

where I explicitly include the coordinates transform Jacobian in the definition of P′ and g′. Then equation (1) is written as

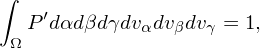(8)

equation (3) is written as

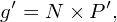(9)

and the number of particle within the phase-space element dαdβdγdv_αdv_βdv_γ is given by

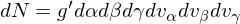(10)

i.e., P′ and g′ act respectively like a probability density function and distribution function in terms of variables (α,β,γ,v_α,v_β,v_γ) with the Jacobian equal to unity (i.e., α,β,β,v_α,v_β,v_γ act as Cartesian coordinates). The reason I do this is as follows. In many simulations, markers are required to be loaded directly in (α,β,γ,v_α,v_β,v_γ) coordinates, i.e., these coordinates are directly sampled. Then working in terms of P′ and g′ is more intuitive to me. In terms of g′, the average phase space volume occupied by a marker is now written as

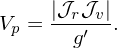(11)

The methods of generating random numbers satisfying a given probability density function are discussed in Sec. 7.

If we use Cartesian coordinates (x,y,z,v_x,v_y,v_z) to describe the phase space, then it is obvious that 𝒥_r = 1 and 𝒥_v = 1.

2.1.1 Time evolution of phase-space volume occupied by a marker

Evaluate V _p at the initial location of each marker and then assign this value, V _pj0, to the corresponding marker, i.e.,

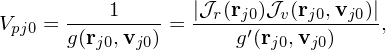(12)

where r_j0 and v_j0 are the initial coordinates of the j th markers.

Further note that any particle distribution function g in any non-relativistic continuous electromagnetic field evolves as dg∕dt = 0, where d∕dt is the convective derivative in the phase space, i.e., the distribution function is constant along a characteristic line. Since V _p = 1∕g, it follows that,

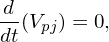(13)

Therefore, V _pj associated with a marker at later time is always equal to the volume initially assigned to it, i.e., V _pj = V _pj0. This is assumed in most collisionless PIC simulation codes and related to the issue of discrete particle noise. In practical simulation, we use finite number rather than infinite number of markers to represent the marker distribution function g. Due to this reason (the so-called discrete particle effect), dg_numerical∕dt is never exactly zero. We can examine how accurate dg_numerical∕dt ≈ 0 is by numerically count the number of markers ΔN in a small phase volume ΔV around a marker and examining the evolution of ΔN∕ΔV . Some choices of the initial state g(x,v,t = 0) can make d(ΔN∕ΔV )∕dt smaller and thus reduce the noise introduced by the discrete particle effect.