Energy conservation (check!)

5.16 Energy conservation (check!)

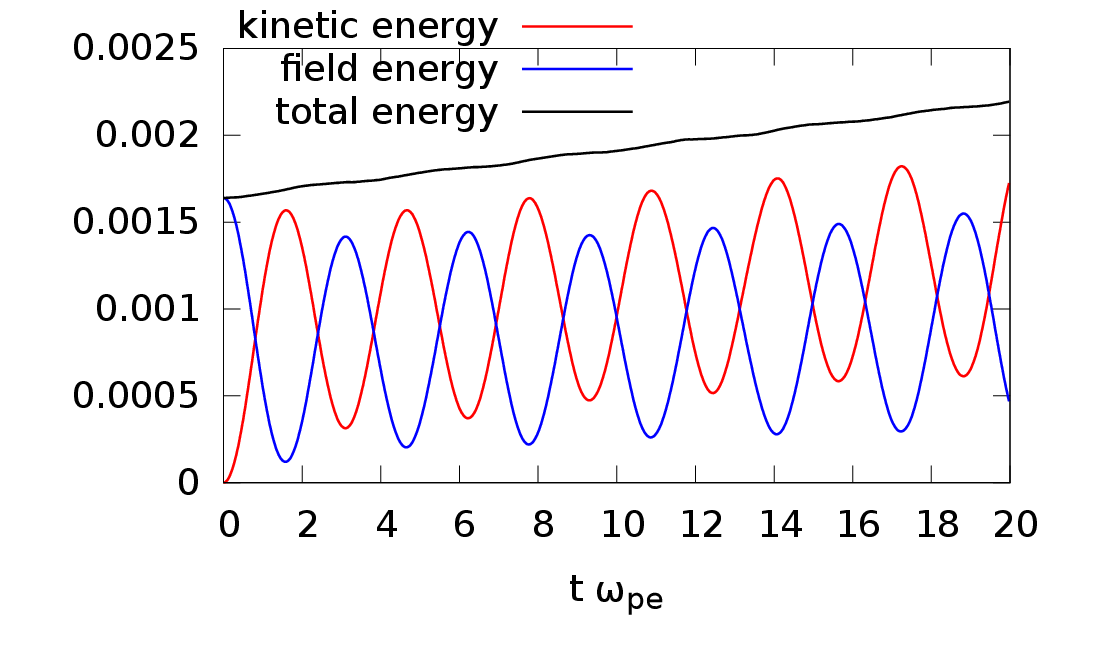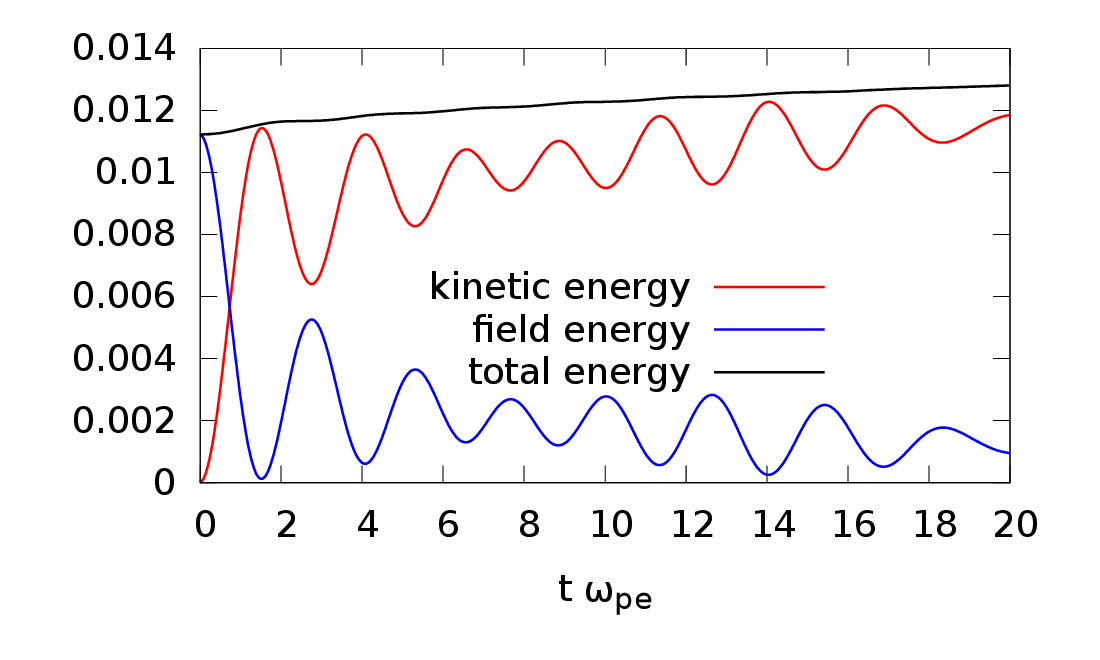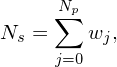
Next we check how well the total energy of the system is conserved in a total-f simulation. The total physical particles in the system is given by

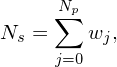N∑p Ns = wj, j=0

(127)

The spatial volume occupied by these physical particles is given by V = N_s∕n₀, where n₀ is the equilibrium electron number density. Since the length along the x direction of the system is L, the cross section S_yz of volume occupied by these physical particles is given by

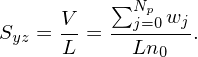∑Np S = V-= --j=0wj-. yz L Ln0

(128)

Then the total electrical energy in the volume is given by

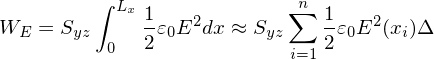∫ Lx 1 2 ∑n 1 2 WE = Syz 0 2𝜀0E dx ≈ Syz 2𝜀0E (xi)Δ i=1

(129)

Deﬁne W₀ = (mv₀²∕2)∑ w_j, and the normalized electric energy W_E = W_E∕W₀, which can be further written as

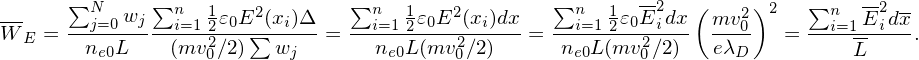∑N ∑n 1 2 ∑n 1 2 ∑n 1 -2 ( 2)2 ∑n -2 -- W-E = --j=0-wj--i=12𝜀0E∑(xi)Δ-= --i=12𝜀0E-(xi)dx= --i=1-2𝜀0Eidx- mv-0 = --i=1-Eidx-. ne0L (mv20∕2) wj ne0L(mv20∕2) ne0L(mv20∕2) eλD L

(130)

The total particle kinetic energy in the system is given by

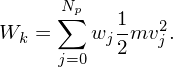∑Np 1 2 Wk = wj2mv j. j=0

(131)

Deﬁne the normalized kinetic energy W_k = W_k∕W₀, which can be further written as

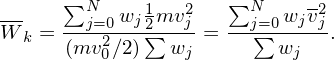∑N 1 2 ∑N -2 W-k = --j=0-wj2∑mv-j= --j=∑0-wjvj. (mv20∕2) wj wj

(132)

Figure 9 plots the time evolution of W_E, W_k −W_k(t = 0), and W_k + W_E −W_k(t = 0), which indicates the total energy is approximately conserved.

pict

Figure 9: Time evolution of the electric energy W_E, kinetic energy W_k, and total energy W_k + W_E −W_k(t = 0). W_k(t = 0) = 0.9991. Full-f simulation without imposing external perturbation.

pict

Figure 10: Time evolution of the electric energy W_E, kinetic energy W_k, and total energy W_k+W_E−W_k(t = 0). Full-f simulation with perturbation w_j−→w_j + 0.05w_j sin(kr_j)

[next] [prev] [prev-tail] [front] [up]