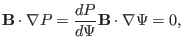Consider the force balance in the direction of
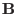 . Dotting the
equilibrium equation (43) by
. Dotting the
equilibrium equation (43) by
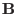 , we obtain
, we obtain
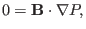 |
(44) |
which implies that 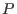 is constant along a magnetic field line. Since
is constant along a magnetic field line. Since  is also constant along a magnetic field line,
is also constant along a magnetic field line, 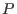 can be expressed in terms of
only
can be expressed in terms of
only  on a single magnetic line. Note that this does not necessarily
mean
on a single magnetic line. Note that this does not necessarily
mean 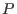 is a single-valued function of
is a single-valued function of  , i.e.
, i.e.
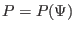 . For
instance,
. For
instance, 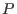 can take different value on different magnetic field lines with
the same value of
can take different value on different magnetic field lines with
the same value of  while still satisfying
while still satisfying
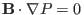 . However, for an asymmetric pressure, it is ready to prove that
. However, for an asymmetric pressure, it is ready to prove that 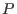 is
indeed a single-valued function of
is
indeed a single-valued function of  on a flux surface since
on a flux surface since  is a
constant on a magnetic surface (however, on different magnetic surfaces with
the same value of
is a
constant on a magnetic surface (however, on different magnetic surfaces with
the same value of  ,
, 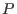 can be different, refer to Sec. 13.8).
On the other hand, if
can be different, refer to Sec. 13.8).
On the other hand, if
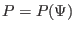 , then we obtain
, then we obtain
i.e., Eq. (44) is satisfied. Therefore
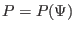 is
equivalent to the force balance equation in the parallel (to the magnetic
field) direction.
is
equivalent to the force balance equation in the parallel (to the magnetic
field) direction.
yj
2018-03-09
![]() . Dotting the
equilibrium equation (43) by
. Dotting the
equilibrium equation (43) by
![]() , we obtain
, we obtain