Toroidal force balance

Next, consider the 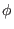$\phi$ component of Eq. (43), which is written

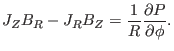$\displaystyle J_Z B_R - J_R B_Z = \frac{1}{R} \frac{\partial P}{\partial \phi} .$

(45)

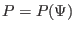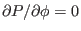Since $P = P (\Psi)$ , which implies $\partial P / \partial \phi = 0$ , equation (45) reduces to

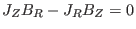$\displaystyle J_Z B_R - J_R B_Z = 0$

(46)

Using the expressions of the poloidal current density (37) and (38) in the force balance equation (46) yields

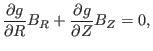$\displaystyle \frac{\partial g}{\partial R} B_R + \frac{\partial g}{\partial Z} B_Z = 0,$

(47)

which can be further written

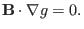$\displaystyle \mathbf{B} \cdot \nabla g = 0.$

(48)

According to the same reasoning for the pressure, we conclude that Eq. (48) is equivalent to 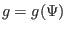$g = g (\Psi)$ . (The function

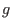defined here is usually called the ``poloidal current function'' in tokamak literature. The reason for this name is discussed in Sec. 2.3.)

yj 2018-03-09