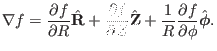Next, we discuss the gauge transformation of the vector potential
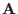 in the axisymmetric case. It is well-known that magnetic field remains the
same under the following gauge transformation:
in the axisymmetric case. It is well-known that magnetic field remains the
same under the following gauge transformation:
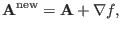 |
(9) |
where 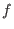 is an arbitrary scalar field. Here we require that
is an arbitrary scalar field. Here we require that 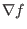 be
axisymmetric because, as mentioned above, an axisymmetric vector potential
suffices for describing an axisymmetric magnetic field. Note that, in
cylindrical coordinates,
be
axisymmetric because, as mentioned above, an axisymmetric vector potential
suffices for describing an axisymmetric magnetic field. Note that, in
cylindrical coordinates, 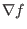 is given by
is given by
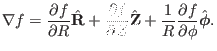 |
(10) |
Since 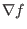 is axisymmetric, it follows that
is axisymmetric, it follows that
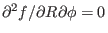 ,
,
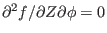 , and
, and
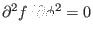 , which implies that
, which implies that
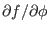 is independent of
is independent of 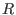 ,
, 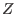 , and
, and 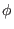 , i.e.,
, i.e.,
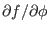 is actually a constant. Using this, the
is actually a constant. Using this, the 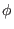 component of
the gauge transformation (9) is written
component of
the gauge transformation (9) is written
where 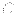 is a constant. Note that the requirement of axial symmetry greatly
reduces the degree of freedom of the gauge transformation for
is a constant. Note that the requirement of axial symmetry greatly
reduces the degree of freedom of the gauge transformation for 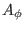 (and
thus for
(and
thus for
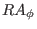 , i..e,
, i..e,  ). Multiplying Eq. (11) with
). Multiplying Eq. (11) with
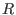 , we obtain the corresponding gauge transformation for
, we obtain the corresponding gauge transformation for  ,
,
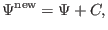 |
(12) |
which indicates  has the same gauge transformation as the familiar
electric potential, i.e., adding a constant. (Note that the definition
has the same gauge transformation as the familiar
electric potential, i.e., adding a constant. (Note that the definition
 does not mean
does not mean
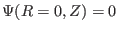 because
because
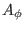 can have a
can have a 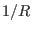 dependence under the gauge transformation
(11)).
dependence under the gauge transformation
(11)).
yj
2018-03-09
![]() in the axisymmetric case. It is well-known that magnetic field remains the
same under the following gauge transformation:
in the axisymmetric case. It is well-known that magnetic field remains the
same under the following gauge transformation: