Magnetic surfaces

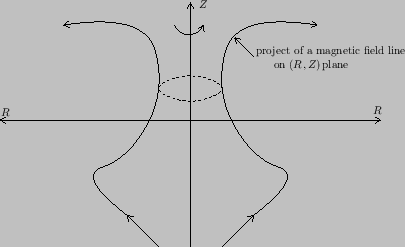
For axial symmetry system, we can define magnetic surfaces in a trivial way (for non-axisymmetric system, the definition may be a little harder, I will consider this later). The axial symmetry of tokamak magnetic field allows us to introduce a surface of revolution that is generated by rotating the projection of a magnetic field line on $(R, Z)$ plane around the axis of symmetry, $Z$ axis. The unique property of this revolution surface is that no field line point-intersects it and a field line with one point on it will have the whole field line on it. This revolution surface is usually called magnetic surface or flux surface. For instance, consider an arbitrary magnetic field line, whose projection on $(R, Z)$ plane is shown in Fig. 1. A magnetic surface is generated by rotating the projection line around the $Z$ axis.

Figure 1: A magnetic surface in tokamak is a revolution surface generated by rotating the projection of a magnetic field line on the $(R, Z)$ plane around the $Z$ axis.

Because $\Psi$ is constant along a magnetic field line and $\Psi$ is independent of $\phi$, it follows that the value of $\Psi$ is constant on a magnetic surface. Therefore $\Psi$ can be used as labels of magnetic surfaces.