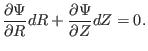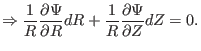Because  is constant along a magnetic field line and
is constant along a magnetic field line and  is
independent of
is
independent of 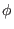 , it follows that the projection of a magnetic field line
onto
, it follows that the projection of a magnetic field line
onto 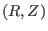 plane is a contour of
plane is a contour of  . On the other hand, it is ready to
prove that the contour of
. On the other hand, it is ready to
prove that the contour of  on
on 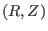 plane is also the projection of a
magnetic field line onto the plane, i.e., a magnetic surface. [Proof. The
contour of
plane is also the projection of a
magnetic field line onto the plane, i.e., a magnetic surface. [Proof. The
contour of  on
on 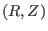 plane is written
plane is written
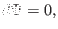 |
(13) |
i.e.,
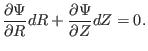 |
(14) |
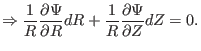 |
(15) |
Using Eqs. (4) and (5), the above equation is written
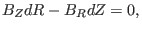 |
(16) |
i.e.,
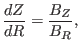 |
(17) |
which is the equation of the projection of a magnetic field line on 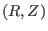 plane. Thus, we prove that the contour of
plane. Thus, we prove that the contour of  is also the projection of a
magnetic field line on
is also the projection of a
magnetic field line on 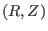 plane.]
plane.]
yj
2018-03-09
![]() is constant along a magnetic field line and
is constant along a magnetic field line and ![]() is
independent of
is
independent of ![]() , it follows that the projection of a magnetic field line
onto
, it follows that the projection of a magnetic field line
onto ![]() plane is a contour of
plane is a contour of ![]() . On the other hand, it is ready to
prove that the contour of
. On the other hand, it is ready to
prove that the contour of ![]() on
on ![]() plane is also the projection of a
magnetic field line onto the plane, i.e., a magnetic surface. [Proof. The
contour of
plane is also the projection of a
magnetic field line onto the plane, i.e., a magnetic surface. [Proof. The
contour of ![]() on
on ![]() plane is written
plane is written