Consider a general coordinate system
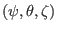 . The metric
tensor is the transformation matrix between the covariant basis vectors and
the contravariant ones. To obtain the metric matrix, we write the contrariant
basis vectors in terms of the covariant ones, such as
. The metric
tensor is the transformation matrix between the covariant basis vectors and
the contravariant ones. To obtain the metric matrix, we write the contrariant
basis vectors in terms of the covariant ones, such as
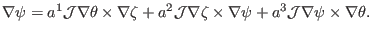 |
(140) |
Taking the scalar product respectively with
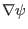 ,
,
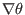 ,
and
,
and
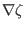 , Eq. (140) is written as
, Eq. (140) is written as
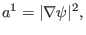 |
(141) |
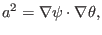 |
(142) |
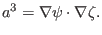 |
(143) |
Similarly, we write
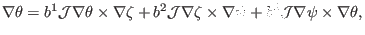 |
(144) |
Taking the scalar product with
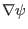 ,
,
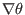 , and
, and
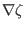 , respectively, the above becomes
, respectively, the above becomes
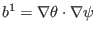 |
(145) |
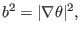 |
(146) |
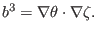 |
(147) |
The same situation applies for the
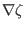 basis vector,
basis vector,
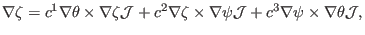 |
(148) |
Taking the scalar product with
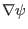 ,
,
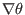 , and
, and
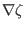 , respectively, the above equation becomes
, respectively, the above equation becomes
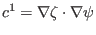 |
(149) |
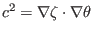 |
(150) |
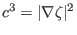 |
(151) |
Summarizing the above results in matrix form, we obtain
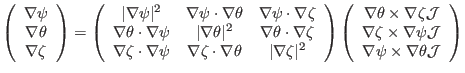 |
(152) |
Similarly, to convert contravariant basis vector to covariant one, we write
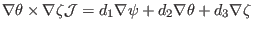 |
(153) |
Taking the scalar product respectively with
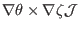 ,
,
 , and
, and
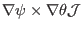 , the above equation becomes
, the above equation becomes
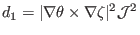 |
(154) |
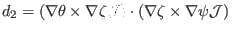 |
(155) |
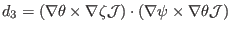 |
(156) |
For the second contravariant basis vector
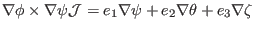 |
(157) |
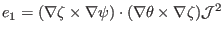 |
(158) |
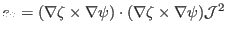 |
(159) |
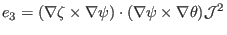 |
(160) |
For the third contravariant basis vector
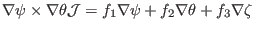 |
(161) |
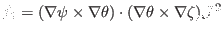 |
(162) |
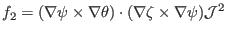 |
(163) |
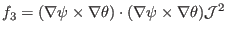 |
(164) |
Summarizing these results, we obtain
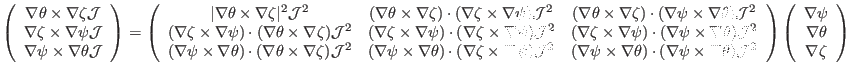 |
(165) |
Note that the matrix in Eqs. (152) and (165) should be the
inverse of each other. It is ready to prove this by directly calculating the
product of the two matrix.
Subsections
yj
2018-03-09
![]() . The metric
tensor is the transformation matrix between the covariant basis vectors and
the contravariant ones. To obtain the metric matrix, we write the contrariant
basis vectors in terms of the covariant ones, such as
. The metric
tensor is the transformation matrix between the covariant basis vectors and
the contravariant ones. To obtain the metric matrix, we write the contrariant
basis vectors in terms of the covariant ones, such as