Next: Covariant and contravariant representation Up: Metric tensor for general Previous: Metric tensor for general
Suppose that
![]() are arbitrary general coordinates except
that
are arbitrary general coordinates except
that ![]() is the usual toroidal angle in cylindrical coordinates. Then
is the usual toroidal angle in cylindrical coordinates. Then
![]() is perpendicular to both
is perpendicular to both
![]() and
and
![]() . Using this, Eq. (152) is simplified to
. Using this, Eq. (152) is simplified to
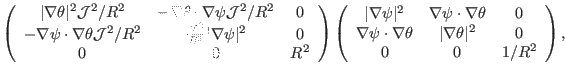 |
(168) |
yj 2018-03-09