The axisymmetric equilibrium magnetic field is given by Eq. (54),
i.e.,
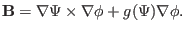 |
(170) |
In
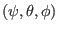 coordinate system, the above expression can be
written as
coordinate system, the above expression can be
written as
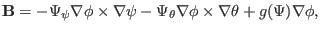 |
(171) |
where the subscripts denote the partial derivatives with the corresponding
subscripts. Note that Eq. (171) is a mixed representation, which
involves both covariant and contravariant basis vectors. Equation
(171) can be converted to contravariant form by using the metric
tensor, giving
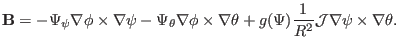 |
(172) |
Similarly, Eq. (171) can also be transformed to covariant form,
giving
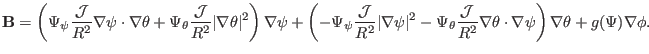 |
(173) |
For the convenience of notation, define
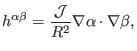 |
(174) |
then Eq. (173) is written as
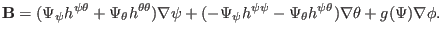 |
(175) |
yj
2018-03-09