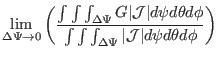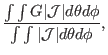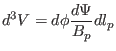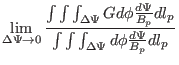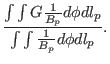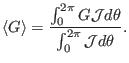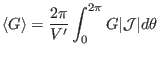Define the magnetic surface average of a physical quantiy  by
by
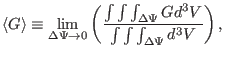 |
(207) |
where the volume integration is over the small volume between two adjacent
flux surfaces with  difference being
difference being
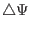 . The differential
volume element is given by
. The differential
volume element is given by
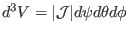 ,
where
,
where
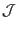 is the Jacobian of
is the Jacobian of
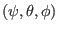 coordinates.
Using this, equation (207) is written as
coordinates.
Using this, equation (207) is written as
which is an averaging over a magnetic surface and thus is called magnetic
surface averaging. Sometimes, we do not want the Jacobian explicitly to appear
in the formula. This can be achived by writing the differential volume element
as
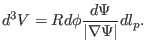 |
(209) |
Using
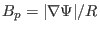 , the volume element is further written as
, the volume element is further written as
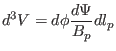 |
(210) |
Using this, the averaging defined in Eq. (207) is written as
If 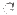 is axisymmetric, then the above equation is written as
is axisymmetric, then the above equation is written as
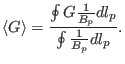 |
(212) |
(Equation (212) is used in the GTAW code to calculate the magnetic
surface averaging.) Using Eq. (188) and
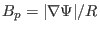 ,
equation (212) can also be written as
,
equation (212) can also be written as
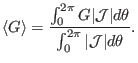 |
(213) |
Noting that the Jacobian does not change sign, the above equation is written
as
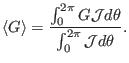 |
(214) |
Using the expression of the volume element
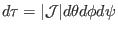 , the volume within a magnetic surface is written
, the volume within a magnetic surface is written
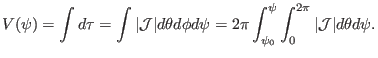 |
(215) |
Using this, the differential of 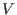 with respect to
with respect to 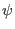 is written as
is written as
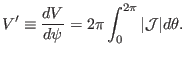 |
(216) |
Using this, Eq. (213) is written as
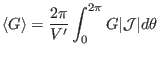 |
(217) |
yj
2018-03-09
![]() by
by