Flux Surface Functions
Next, examine the meaning of the following volume integral
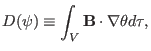 |
(218) |
where the volume
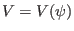 , which is the volume within the magnetic
surface labeled by
, which is the volume within the magnetic
surface labeled by 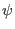 . Using
. Using
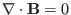 , the quantity
, the quantity
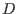 can be further written as
can be further written as
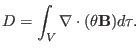 |
(219) |
Note that  is not a single-value function of the spacial points. In
order to evaluate the integration in Eq. (219), we need to select
one branch of
is not a single-value function of the spacial points. In
order to evaluate the integration in Eq. (219), we need to select
one branch of  , which can be chosen to be
, which can be chosen to be
 . Note that function
. Note that function
 is not continuous in the
vicinity of the contour of
is not continuous in the
vicinity of the contour of
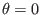 . Next, we want to use the Gauss's
theorem to convert the above volume integration to surface integration. Noting
the discontinuity of the integrand
. Next, we want to use the Gauss's
theorem to convert the above volume integration to surface integration. Noting
the discontinuity of the integrand
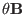 in the vicinity of the
contour of
in the vicinity of the
contour of
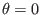 , the volume should be cut along the contour, thus,
generating two surfaces. Denote these two surfaces by
, the volume should be cut along the contour, thus,
generating two surfaces. Denote these two surfaces by 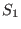 and
and 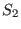 , then
equation (219) is written as
, then
equation (219) is written as
where the direction of surface 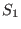 is in the negative direction of
is in the negative direction of  ,
the direction of
,
the direction of 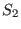 is in the positive direction of
is in the positive direction of  , and the
surface
, and the
surface 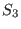 is the toroidal magnetic surface
is the toroidal magnetic surface
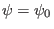 . The surface
integration through
. The surface
integration through 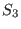 is obviously zero since
is obviously zero since
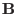 lies in this
surface. Therefore, we have
lies in this
surface. Therefore, we have
Eq. (220) indicates that 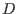 is
is 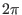 times the magnetic flux
through the
times the magnetic flux
through the 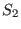 surface. Thus, the poloidal flux through
surface. Thus, the poloidal flux through 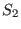 is written as
is written as
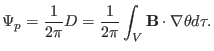 |
(221) |
Using the expression of the volume element
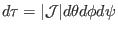 ,
, 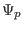 can be further written in terms of flux surface
averaged quantities.
can be further written in terms of flux surface
averaged quantities.
Note that the sign of the Jacobian appears in Eq. (222), which is
due to the positive direction of surface 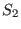 is determined by the positive
direction of
is determined by the positive
direction of  , which in turn is determined by the sign of the Jacobian
(In my code, however, the positive direction of
, which in turn is determined by the sign of the Jacobian
(In my code, however, the positive direction of  is chosen by me and
the sign of the Jacobian is determined by the positive direction of
is chosen by me and
the sign of the Jacobian is determined by the positive direction of  ).
We can verify the sign of Eq. (222) is exactly consistent with that
in Eq. (19).
).
We can verify the sign of Eq. (222) is exactly consistent with that
in Eq. (19).
Similarly, the toroidal flux within a flux surface is written as
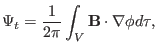 |
(223) |
the poloidal current within a flux surface is written as
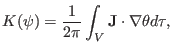 |
(224) |
and toroidal current within a flux surface is written as
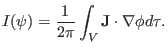 |
(225) |
(**check**)The toroidal magnetic flux is written as
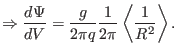 |
(227) |
Next, calculate the derivative of the toroidal flux with respect to the
poloidal flux.
Comparing this result with Eq. (471) indicates that it is equal to
the safety factor, i.e.,
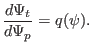 |
(229) |
By using the contravariant representation of current density (331),
the poloidal current within a magnetic surface is written as
Note that the poloidal current is proportional to 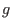 , which explains why
, which explains why 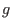 is sometimes called poloidal current function in tokamak literature.
is sometimes called poloidal current function in tokamak literature.
The toroidal current is written as
The last equality is due to
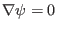 at
at 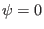 . By using the flux
surface average operator, Eq. (231) is written
. By using the flux
surface average operator, Eq. (231) is written
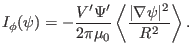 |
(232) |
Next, calculate another useful surface-averaged quantity,
The differential with respect to 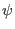 and the integration with respect to
and the integration with respect to
 can be interchanged, yielding
can be interchanged, yielding
yj
2018-03-09
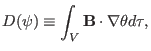
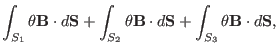
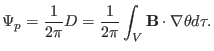
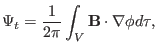
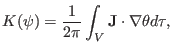
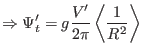
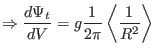
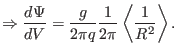
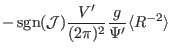
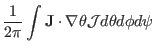
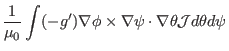
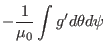
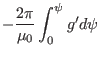
![$\displaystyle - \left[ \left( \Psi' \frac{\mathcal{J}}{R^2} \vert \nabla \psi \...
...\right] \nabla \psi \times \nabla \theta -
g' \nabla \phi \times \nabla \psi, $](img737.png)
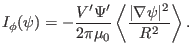
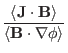
![$\displaystyle \frac{\left\langle \frac{g^2}{\mathcal{J}} \left[
\left( \frac{1}...
...J}}{R^2} \right)_{\theta} \right] \right\rangle}{\mu_0
\langle g / R^2 \rangle}$](img749.png)
![$\displaystyle \frac{\frac{2 \pi}{V'} \int_0^{2 \pi} d \theta g^2 \left[ \left(
...
...ac{\mathcal{J}}{R^2} \right)_{\theta} \right]}{\mu_0 g \langle R^{- 2}
\rangle}$](img750.png)
![$\displaystyle \frac{\frac{2 \pi}{V'} g^2 \int_0^{2 \pi} d \theta \left[ \left(
...
...ac{\mathcal{J}}{R^2} \right)_{\theta} \right]}{\mu_0 g \langle R^{- 2}
\rangle}$](img751.png)
![$\displaystyle \frac{\frac{2 \pi}{V'} g \int_0^{2 \pi} d \theta \left[ \left(
\f...
...vert \nabla \psi \vert^2 \right)_{\psi}
\right]}{\mu_0 \langle R^{- 2} \rangle}$](img752.png)
![$\displaystyle \frac{\frac{2 \pi}{V'} g \int_0^{2 \pi} d \theta \left[ \left(
\f...
...vert \nabla \psi \vert^2 \right)_{\psi}
\right]}{\mu_0 \langle R^{- 2} \rangle}$](img752.png)
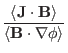
![$\displaystyle \frac{\frac{2 \pi}{V'} g \left[ \frac{1}{g} \Psi'
\left( \int_0^{...
...vert \nabla \psi \vert^2
\right) \right]_{\psi}}{\mu_0 \langle R^{- 2} \rangle}$](img753.png)
![$\displaystyle \frac{\frac{1}{V'} g \left[ \frac{1}{g} \Psi' V' \left\langle \fr...
...\psi \vert^2}{R^2} \right\rangle \right]_{\psi}}{\mu_0 \langle R^{- 2}
\rangle}$](img754.png)
![$\displaystyle \frac{g}{\mu_0 V' \langle R^{- 2} \rangle} \left[ \frac{\Psi' V'}...
...\left\langle \frac{\vert \nabla \psi \vert^2}{R^2} \right\rangle \right]_{\psi}$](img755.png)