Next: Contravariant form of magnetic Up: Magnetic surface coordinates general Previous: Magnetic surface coordinates general
In Sec. 5.1, we introduced the local safety factor ![]() .
Equation (179) indicates that if the Jacobian is chosen to be of the
form
.
Equation (179) indicates that if the Jacobian is chosen to be of the
form
![]() , where
, where
![]() is an arbitrary
function of
is an arbitrary
function of ![]() , then the local safety factor is independent of
, then the local safety factor is independent of ![]() and
and ![]() , i.e., magnetic line is straight in
, i.e., magnetic line is straight in
![]() plane. On the
other hand, if we want to make field line straight in
plane. On the
other hand, if we want to make field line straight in
![]() plane,
the Jacobian must be chosen to be of the specific form
plane,
the Jacobian must be chosen to be of the specific form
![]() . We note that, as mentioned in Sec. 5.2, the poloidal
angle is fully determined by the choice of the Jacobian. The specific choice
of
. We note that, as mentioned in Sec. 5.2, the poloidal
angle is fully determined by the choice of the Jacobian. The specific choice
of
![]() is usually too restrictive for choosing a
desired poloidal angle (for example, the equal-arc poloidal angle can not be
achieved by this choice of Jacobian). Is there any way that we can make the
field line straight in a coordinate system at the same time ensure that the
Jacobian can be freely adjusted to obtain desired poloidal angle? The answer
is yes. The obvious way to achieve this is to define a new toroidal angle
is usually too restrictive for choosing a
desired poloidal angle (for example, the equal-arc poloidal angle can not be
achieved by this choice of Jacobian). Is there any way that we can make the
field line straight in a coordinate system at the same time ensure that the
Jacobian can be freely adjusted to obtain desired poloidal angle? The answer
is yes. The obvious way to achieve this is to define a new toroidal angle
![]() that generalizes the usual toroidal angle
that generalizes the usual toroidal angle ![]() . Define the new
toroidal angle
. Define the new
toroidal angle ![]() as[6]
as[6]
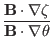 |
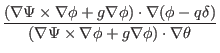 |
||
![$\displaystyle \frac{(\nabla \Psi \times \nabla \phi + g \nabla \phi) \cdot [\na...
...phi - \nabla (q \delta)]}{(\nabla \Psi \times \nabla \phi) \cdot \nabla
\theta}$](img763.png) |
|||
![$\displaystyle \frac{g \vert \nabla \phi \vert^2 + (\nabla \Psi \times \nabla \p...
... [-
\nabla (q \delta)]}{(\nabla \Psi \times \nabla \phi) \cdot \nabla \theta} .$](img764.png) |
(236) |
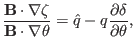 |
(238) |
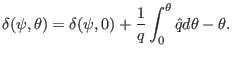 |
(241) |
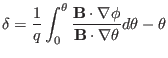 |
(243) |
In summary, the field line is straight (with slope being ![]() ) on
) on
![]() plane if
plane if ![]() is defined by Eq. (244). In this method,
we make the field line straight by defining a new toroidal angle, instead of
requiring the Jacobian to take particular forms. Thus, the freedom of choosing
the form of the Jacobian is still available to be used later to define a good
poloidal angle coordinate.
is defined by Eq. (244). In this method,
we make the field line straight by defining a new toroidal angle, instead of
requiring the Jacobian to take particular forms. Thus, the freedom of choosing
the form of the Jacobian is still available to be used later to define a good
poloidal angle coordinate.
[In numerical implementation, the term
![]() appearing in
appearing in ![]() is computed by using
is computed by using
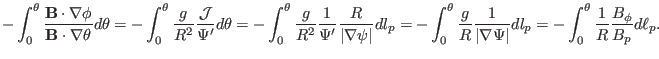 |
(245) |
![[*]](crossref.png) ), we obtain
), we obtain
It is ready to see that the function
![]() , which is
introduced above to make
, which is
introduced above to make
![]() , satisfies the periodic condition
, satisfies the periodic condition
![]() . [Proof: Equation (242) implies that
. [Proof: Equation (242) implies that
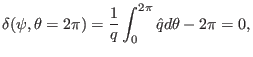 |
(247) |
yj 2018-03-09