Closed magnetic surfaces in tokamak

In most part of a tokamak plasma, the contours of $\Psi$ on $(R, Z)$ plane are closed curves. As discussed above, the contours of $\Psi$ are the projection of magnetic lines on the poloidal plane. Closed contours of $\Psi$ implies closed magnetic surfaces, as shown in Fig 3.

Figure 3: Closed magnetic surfaces (blue) and various toroidal surfaces used to define the poloidal magnetic flux. The magnetic flux through the toroidal surface $S_2$ and $S_3$ is equal to each other. Also the magnetic flux through $S_4$ and $S_5$ is equal to each other; the magnetic flux through $S_0$ and $S_1$ is equal to each other.

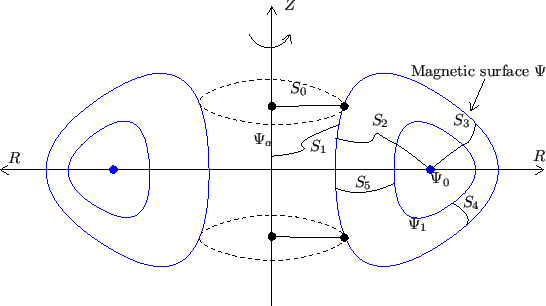The innermost magnetic surface is actually a line, which is usually called the magnetic axis (in Fig. 3, $\Psi_0$ labels the magnetic axis). Because the magnetic axis is the point of maximum/minimum of $\Psi (R, Z)$, the value of $\nabla \Psi$ is zero at the magnetic axis. As a result, the poloidal component of the equilibrium magnetic field is zero on magnetic axis (refer to Eq. (8)), i.e., the magnetic field has only toroidal component there.

As discussed in Sec. 1.4, the poloidal magnetic flux enclosed by a magnetic surface $\Psi$ (the poloidal magnetic flux through the toroidal surfaces $S_2$) is given by

$$\Psi_p = 2 \pi (\Psi_0 - \Psi),$$ (19)

where $\Psi_0$ is the value of $\Psi$ at the magnetic axis. Here the positive direction of the surface $S_2$ is defined to be in the clockwise direction when an observer looks along the direction of $\hat{\ensuremath{\boldsymbol{\phi}}}$. In practice, we need to pay attention to the positive direction of the toroidal surface used to define the poloidal flux (there can be a sign difference when choosing different positive directions). Also note, in tokamak literature, the poloidal magnetic flux enclosed by a closed magnetic surface can have two different definitions, one of which is the the poloidal magnetic flux through the surface $S_2$ in Fig. 3, the other one is the poloidal magnetic flux through the central hole of the magnetic surface, i.e., the poloidal flux through $S_1$ in Fig. 3. The former definition is adopted in this article, except explicitly specified otherwise. In the latter case, the poloidal magnetic flux is written

$$\Psi_p = 2 \pi (\Psi - \Psi_a),$$ (20)

where the positive direction of the surface $S_1$ is defined to be in the clockwise direction.

Also note that, since the poloidal magnetic field can be written as $\mathbf{B}_p = \nabla \Psi \times \nabla \phi$, the condition $\Psi_{\ensuremath{\operatorname{LCFS}}} - \Psi_{\ensuremath{\operatorname{axis}}} > 0$ means $\mathbf{B}_p$ points in the anticlockwise direction (viewed along $\ensuremath{\boldsymbol{\phi}}$ direction), and $\Psi_{\ensuremath{\operatorname{LCFS}}} - \Psi_{\ensuremath{\operatorname{axis}}} < 0$ means $\mathbf{B}_p$ points in the clockwise direction.