Next: Field-line-following coordinates Up: Magnetic surface coordinates general Previous: Form of operator in
In solving the MHD eigenmode equations in toroidal geometry, we also need the
radial differential operator
![]() . Next, we derive the
form of the operator in
. Next, we derive the
form of the operator in
![]() coordinates. Using
coordinates. Using
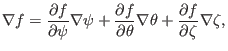
![$\displaystyle \nabla \psi \cdot \nabla \zeta = - \left[ \frac{\partial (q \delt...
...rac{\partial \delta}{\partial \theta} \nabla \theta \cdot \nabla \psi \right] .$](img872.png) |
(274) |
yj 2018-03-09