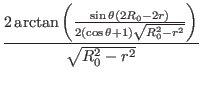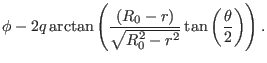For the above magnetic field, the toroidal shift involved in the definition of
the generalized toroidal angle can be evaluated analytically. The toroidal
shift is given by
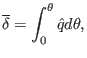 |
(353) |
where the local safety factor 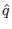 can be written as
can be written as
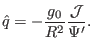 |
(354) |
Using
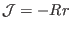 and
and
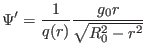 |
(355) |
The local safety factor 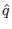 in Eq. (354) is written as
in Eq. (354) is written as
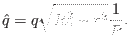 |
(356) |
Using this, expression (353) is written
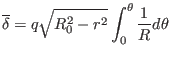 |
(357) |
The integration
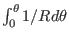 can be evaluated explicitly
(using maxima), yielding
can be evaluated explicitly
(using maxima), yielding
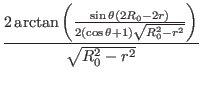 |
(358) |
Then expression (357) is written
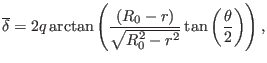 |
(359) |
where use has been made of
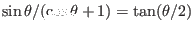 . Using this, the generalized toroidal angle can be written as
. Using this, the generalized toroidal angle can be written as
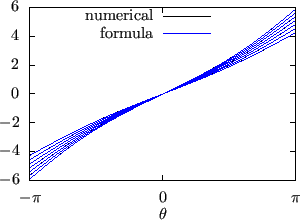
The results given by the formula (359) are compared with the
results from my code that assumes a general numerical configuration. The
results from the two methods agree with each other, as is shown in Fig.
27, which provides confidence in both the analytical formula and
the numerical code.
Figure:
The results of
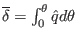 computed by using formula
(359) and the numerical code agree with each other. The
different lines correspond to different magnetic surfaces.
computed by using formula
(359) and the numerical code agree with each other. The
different lines correspond to different magnetic surfaces.
 |
yj
2018-03-09