Next: Safety factor profile Up: Magnetic configuration with concentric-circular Previous: Explicit expression for the
Let ![]() and define
and define
![]() ,
,
![]() , etc. Explicit
expressions for these elements can be written as
, etc. Explicit
expressions for these elements can be written as
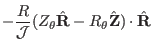 |
|||
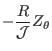 |
|||
| (361) |
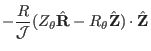 |
|||
| 0 |
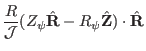 |
|||
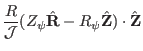 |
|||
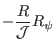 |
|||
| 0 |
![$\displaystyle \left[ \frac{\hat{\ensuremath{\boldsymbol{\phi}}}}{R} + \left( \f...
...\mathcal{J}}
R_{\theta} \right) \hat{\mathbf{Z}} \right] \cdot \hat{\mathbf{R}}$](img1167.png) |
|||
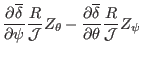 |
|||
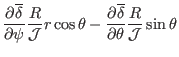 |
|||
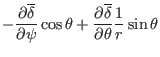 |
|||
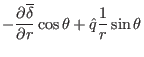 |
![$\displaystyle \left[ \frac{\hat{\ensuremath{\boldsymbol{\phi}}}}{R} + \left( \f...
...\mathcal{J}}
R_{\theta} \right) \hat{\mathbf{Z}} \right] \cdot \hat{\mathbf{Z}}$](img1174.png) |
|||
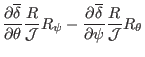 |
|||
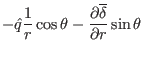 |
| (362) |
![$\displaystyle 2 \frac{d q}{d r} \arctan \left(
\frac{(R_0 - r)}{\sqrt{R_0^2 - r...
...a}{2}
\right) \frac{d}{d r} \left[ \frac{(R_0 - r)}{\sqrt{R_0^2 - r^2}} \right]$](img1180.png) |
|||
 |
yj 2018-03-09