Assume magnetic surfaces of a magnetic configuration are given by
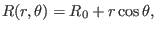 |
(333) |
and
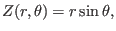 |
(334) |
where 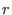 is the label of magnetic surfaces (i.e.,
is the label of magnetic surfaces (i.e.,
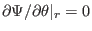 ). The above parametric equations specify a series
of concentric-circular magnetic surfaces with
). The above parametric equations specify a series
of concentric-circular magnetic surfaces with 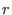 being the minor radius.
being the minor radius.
Assume the poloidal plasma current is zero, i.e.,
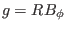 is a
constant (this constant is denoted by
is a
constant (this constant is denoted by 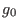 in the following). In this case
the toroidal magnetic field is determined by
in the following). In this case
the toroidal magnetic field is determined by
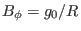 . Assume the
. Assume the
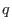 profile is given. Next, let us determine the poloidal magnetic field
profile is given. Next, let us determine the poloidal magnetic field
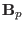 , which is given by
, which is given by
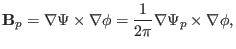 |
(335) |
which involves the poloidal magnetic flux 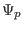 . Our task is to express the
poloidal magnetic flux
. Our task is to express the
poloidal magnetic flux 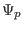 in terms of
in terms of 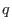 and
and 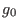 . Using
. Using
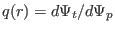 , we obtain
, we obtain
Integrate the above equation over 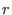 , we obtain
, we obtain
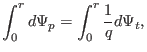 |
(336) |
which an be written as
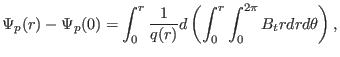 |
(337) |
where use has been made of
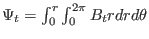 . Using
. Using
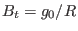 and
and
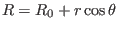 , the above
equation is written
, the above
equation is written
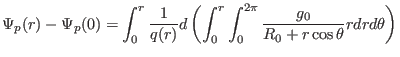 |
(338) |
Using maxima (an open-source computer algebra system), the above integration
over  can be performed analytically, giving
can be performed analytically, giving
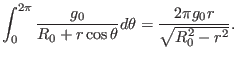 |
(339) |
Using this, equation (338) is written as
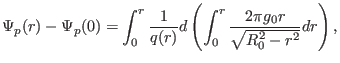 |
(340) |
which can be simplified as
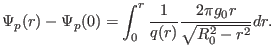 |
(341) |
Using this, the poloidal magnetic field in Eq. (335) is written
as
[Using the formulas
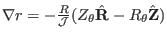 and
and
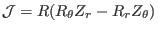 , we obtain
, we obtain
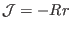 and
and
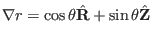 ,
,
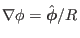 . Then Eq. (342) is
written as
. Then Eq. (342) is
written as
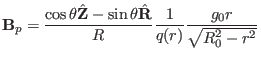 |
(343) |
This is the formula for calculating the poloidal magnetic field. The magnitude
of
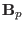 is written as
is written as
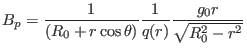 |
(344) |
Note that both 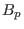 and
and 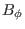 depend on the poloidal angle
depend on the poloidal angle  .]
.]
I use Eq. (341) to compute the 2D data of  (
(
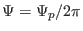 ) on the poloidal plane when creating a numerical G-eqdsk file for the
above equilibrium.
) on the poloidal plane when creating a numerical G-eqdsk file for the
above equilibrium.
Subsections
yj
2018-03-09
![]() is a
constant (this constant is denoted by
is a
constant (this constant is denoted by ![]() in the following). In this case
the toroidal magnetic field is determined by
in the following). In this case
the toroidal magnetic field is determined by
![]() . Assume the
. Assume the
![]() profile is given. Next, let us determine the poloidal magnetic field
profile is given. Next, let us determine the poloidal magnetic field
![]() , which is given by
, which is given by
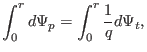
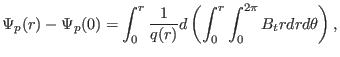
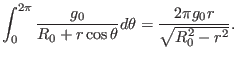
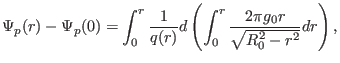
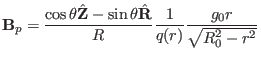
![]() (
(
![]() ) on the poloidal plane when creating a numerical G-eqdsk file for the
above equilibrium.
) on the poloidal plane when creating a numerical G-eqdsk file for the
above equilibrium.