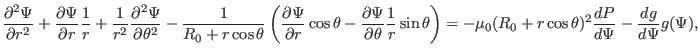Next: Large aspect ratio expansion Up: Notes on tokamak equilibrium Previous: Safety factor profile
Consider
![]() coordinates, which are related to the cylindrical
coordinates
coordinates, which are related to the cylindrical
coordinates ![]() by
by
![]() and
and
![]() , as
shown in Fig. 28.
, as
shown in Fig. 28.
Next, we transform the GS equation from ![]() coordinates to
coordinates to
![]() coordinates. Using the relations
coordinates. Using the relations
![]() and
and
![]() , we have
, we have
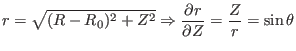 |
(369) |
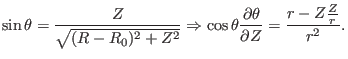 |
(370) |
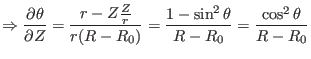 |
(371) |
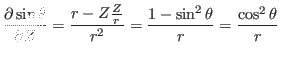 |
(372) |
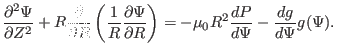 |
(373) |
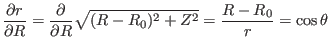 |
(376) |
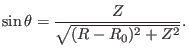
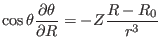
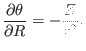 |
(377) |
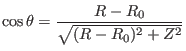
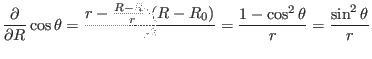 |
(378) |
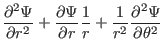 |
(381) |